题目内容
已知函数f(x)=ex-x2+a,x∈R的图象在点x=0处的切线为y=bx.(e≈2.71828).
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)g(x)=
,x∈(0,+∞),讨论函数g(x)的单调性与极值;
(Ⅲ)若k∈Z,且f(x)+
(3x2-5x-2k)≥0 对任意x∈R恒成立,求k的最大值.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)g(x)=
| f(x) |
| x |
(Ⅲ)若k∈Z,且f(x)+
| 1 |
| 2 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由导数的几何意义,列出方程组求得a,b的值即可;
(Ⅱ)利用导数与函数的单调性、极值的关系,即可求得结论;
(Ⅲ)由f(x)+
(3x2-5x-2k)≥0 对任意x∈R恒成立,?k≤ex+
x2-
x-1对任意x∈R恒成立.
令h(x)=ex+
x2-
x-1,利用导数求得函数h(x)的最小值即可求得结论.
(Ⅱ)利用导数与函数的单调性、极值的关系,即可求得结论;
(Ⅲ)由f(x)+
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
令h(x)=ex+
| 1 |
| 2 |
| 5 |
| 2 |
解答:
解:(Ⅰ)f(x)=ex-x2+a,f'(x)=ex-2x.
由已知
⇒
,f(x)=ex-x2-1.…(4分)
(Ⅱ)由(Ⅰ)知,g(x)=
, x>0,
则g′(x)=
=
=
.
令y=ex-x-1,y'=ex-1>0在x∈(0,+∞)恒成立,
从而y=ex-x-1在(0,+∞)上单调递增,y>e0-0-1=0.
令g'(x)>0,得x>1;g'(x)<0,得0<x<1.
∴g(x)的增区间为(1,+∞),减区间为(0,1).极小值为g(1)=e-2,无极大值.…(8分)
(Ⅲ)f(x)+
(3x2-5x-2k)≥0对任意x∈R恒成立,?ex+
x2-
x-1-k≥0对任意x∈R恒成立,
?k≤ex+
x2-
x-1对任意x∈R恒成立.…(10分)
令h(x)=ex+
x2-
x-1,h′(x)=ex+x-
,易知h'(x)在R上单调递增,
又h′(0)=-
<0,h′(1)=e-
>0,h′(
)=e
-2<0,h′(
)=e
-
>2.56
-
=1.6
-
=
-
>2-
=
>0,
∴存在唯一的x0∈(
,
),使得h'(x0)=0,…(12分)
且当x∈(-∞,x0)时,h'(x)<0,x∈(x0,+∞)时,h'(x)>0.
即h(x)在(-∞,x0)单调递减,在(x0,+∞)上单调递增,h(x)min=h(x0)=ex0+
-
x0-1,
又h'(x0)=0,即ex0+x0-
=0,ex0=
-x0.
∴h(x0)=
-x0+
-
x0-1=
(
-7x0+3),
∵x0∈(
,
),∴h(x0)∈(-
, -
).k≤ex+
x2-
x-1对任意x∈R恒成立,
?k≤h(x0),又k∈Z,∴kmax=-1.…(14分)
由已知
|
|
(Ⅱ)由(Ⅰ)知,g(x)=
| f(x) |
| x |
则g′(x)=
| xf′(x)-f(x) |
| x2 |
| x(ex-2x)-(ex-x2-1) |
| x2 |
| (x-1)(ex-x-1) |
| x2 |
令y=ex-x-1,y'=ex-1>0在x∈(0,+∞)恒成立,
从而y=ex-x-1在(0,+∞)上单调递增,y>e0-0-1=0.
令g'(x)>0,得x>1;g'(x)<0,得0<x<1.
∴g(x)的增区间为(1,+∞),减区间为(0,1).极小值为g(1)=e-2,无极大值.…(8分)
(Ⅲ)f(x)+
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
?k≤ex+
| 1 |
| 2 |
| 5 |
| 2 |
令h(x)=ex+
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
又h′(0)=-
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 4 |
| 3 |
| 4 |
| 7 |
| 4 |
| 3 |
| 2 |
| 7 |
| 4 |
|
| 7 |
| 4 |
| 7 |
| 4 |
| 1 |
| 4 |
∴存在唯一的x0∈(
| 1 |
| 2 |
| 3 |
| 4 |
且当x∈(-∞,x0)时,h'(x)<0,x∈(x0,+∞)时,h'(x)>0.
即h(x)在(-∞,x0)单调递减,在(x0,+∞)上单调递增,h(x)min=h(x0)=ex0+
| 1 |
| 2 |
| x | 2 0 |
| 5 |
| 2 |
又h'(x0)=0,即ex0+x0-
| 5 |
| 2 |
| 5 |
| 2 |
∴h(x0)=
| 5 |
| 2 |
| 1 |
| 2 |
| x | 2 0 |
| 5 |
| 2 |
| 1 |
| 2 |
| x | 2 0 |
∵x0∈(
| 1 |
| 2 |
| 3 |
| 4 |
| 27 |
| 32 |
| 1 |
| 8 |
| 1 |
| 2 |
| 5 |
| 2 |
?k≤h(x0),又k∈Z,∴kmax=-1.…(14分)
点评:本题主要考查利用导数研究函数的单调性、极值、最值等知识,考查学生的分析问题,解决问题的能力及运算求解能力,考查等价转化思想的运用,综合性强,属难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
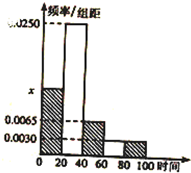 某公司对夏季室外工作人员规定如下:当气温超过35℃时,室外连续工作时间严禁超过100分钟;不少于60分钟的,公司给予适当补助.随机抽取部分工人调查其高温室外连续工作时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中工作时间范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某公司对夏季室外工作人员规定如下:当气温超过35℃时,室外连续工作时间严禁超过100分钟;不少于60分钟的,公司给予适当补助.随机抽取部分工人调查其高温室外连续工作时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中工作时间范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].