题目内容
6.设全集U={-1,1,3,5,7},集合A={1,|3-a|,5},若∁UA={-1,7},则实数a的值是( )| A. | 0 | B. | 6 | C. | -4或10 | D. | 0或6 |
分析 根据补集的定义得到关于a的方程,求出a的值即可.
解答 解:U={-1,1,3,5,7},
A={1,|3-a|,5},若∁UA={-1,7},
则|3-a|=3,解得:a=0或6,
故选:D.
点评 本题考查了集合的补集的运算,考查解绝对值方程,是一道基础题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
11.如果一个数列的前5项分别是1,2,3,4,5,则下列说法正确的是( )
| A. | 该数列一定是等差数列 | B. | 该数列一定不是等差数列 | ||
| C. | 该数列不一定是等差数列 | D. | 以上结论都不正确 |
16.
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.参考公式:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
(3)当销售额为4(千万元)时,估计利润额的大小.
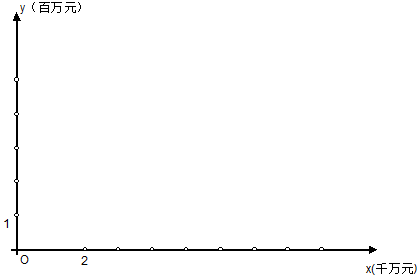
| 商品名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.参考公式:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
(3)当销售额为4(千万元)时,估计利润额的大小.

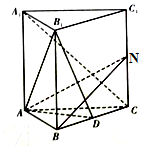 在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=$\sqrt{2}$,且D为BC中点.
在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=$\sqrt{2}$,且D为BC中点.