题目内容
7.命题:“对任意 x>0,ex>x+1”的否定是( )| A. | 存在 x≤0,ex≤x+1 | B. | 存在 x>0,ex≤x+1 | ||
| C. | 存在 x≤0,ex>x+1 | D. | 对任意 x>0,ex≤x+1 |
分析 利用全称命题的否定是特称命题,写出结果即可.
解答 解:因为全称命题的否定是特称命题,所以,命题:“对任意 x>0,ex>x+1”的否定是:存在 x>0,ex≤x+1.
故选:B.
点评 本题考查命题的否定,特称命题与全称命题的否定关系,是基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
12.若tanθ=2,则$\frac{2sinθ-cosθ}{sinθ+2cosθ}$的值为( )
| A. | 0 | B. | 1 | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
16.
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.参考公式:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
(3)当销售额为4(千万元)时,估计利润额的大小.
| 商品名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.参考公式:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
(3)当销售额为4(千万元)时,估计利润额的大小.

 正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.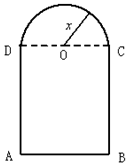 如图,用长为12m的铁丝弯成下部为矩形,上部为半圆形的框架窗户,若半圆半径
如图,用长为12m的铁丝弯成下部为矩形,上部为半圆形的框架窗户,若半圆半径