题目内容
2.若函数f(x)是定义在R上的偶函数,在(-∞,0)上对任意两个不相等的实数a,b总有$\frac{f(a)-f(b)}{a-b}$>0,且f(2)=0,则使xf(x)<0的x的取值范围是( )| A. | -2<x<2 | B. | x>2或-2<x<0 | C. | -2<x<0 | D. | x<-2或x>2 |
分析 由题意可得偶函数f(x)在(-∞,0)上单调递增,故它在(0,+∞)上单调递减,通过讨论x的范围,求出不等式xf(x)的解集即可.
解答 解:f(x)是定义在R上的偶函数,
且对任意的a,b∈(-∞,0),
当a≠b时,都有$\frac{f(a)-f(b)}{a-b}$>0,
故函数f(x)在(-∞,0]上单调递增,
故它在(0,+∞)上单调递减.
故x>0时,xf(x)<0,即f(x)<f(2),解得:x>2,
x<0时,xf(x)<0,即f(x)>f(-2),解得:-2<x<0,
故选:B.
点评 本题主要考查函数的单调性和奇偶性的应用,是一道中档题.

练习册系列答案
相关题目
12.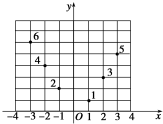 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示.
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示.
按如此规律下去,则a2009+a2010+a2011等于( )
 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示.
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示.| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
| A. | 1 003 | B. | 1 005 | C. | 1 006 | D. | 2 010 |
7.同时掷两颗骰子,计算向上的点数和为5的概率为( )
| A. | $\frac{1}{36}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{6}$ |
11.如果一个数列的前5项分别是1,2,3,4,5,则下列说法正确的是( )
| A. | 该数列一定是等差数列 | B. | 该数列一定不是等差数列 | ||
| C. | 该数列不一定是等差数列 | D. | 以上结论都不正确 |
12.若tanθ=2,则$\frac{2sinθ-cosθ}{sinθ+2cosθ}$的值为( )
| A. | 0 | B. | 1 | C. | $\frac{3}{4}$ | D. | $\frac{5}{4}$ |
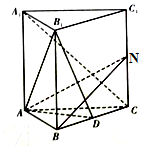 在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=$\sqrt{2}$,且D为BC中点.
在直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=$\sqrt{2}$,且D为BC中点.