题目内容
已知
=(-3,4),|
|=2,
与
的夹角为60°,
=2
-
,
=
+k
,当实数k为何值时,
(1)
⊥
;
(2)
∥
.
| a |
| b |
| a |
| b |
| m |
| a |
| b |
| n |
| a |
| b |
(1)
| m |
| n |
(2)
| m |
| n |
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:(1)利用数量积的定义及其运算性质、向量垂直与数量积的关系即可得出;
(2)利用向量共线定理即可得出.
(2)利用向量共线定理即可得出.
解答:
解:(1)∵
=(-3,4),|
|=2,
与
的夹角为60°,
∴|
|=5,
•
=5×2×cos60°=5.
∵
⊥
,∴
•
=(2
-
)•(
+k
)=0,
化为2
2-k
2+(2k-1)
•
=0,
∴2×52-4k+5(2k-1)=0,解得k=-
.
∴当k=-
时,
⊥
.
(2)∵
∥
,∴存在实数λ使得
=λ
,
∴2
-
=λ(
+k
),
化为(2-λ)
-(1+λk)
=
,
∵
与
不共线,∴
,解得k=-
.
∴当k=-
时,
∥
.
| a |
| b |
| a |
| b |
∴|
| a |
| a |
| b |
∵
| m |
| n |
| m |
| n |
| a |
| b |
| a |
| b |
化为2
| a |
| b |
| a |
| b |
∴2×52-4k+5(2k-1)=0,解得k=-
| 15 |
| 2 |
∴当k=-
| 15 |
| 2 |
| m |
| n |
(2)∵
| m |
| n |
| m |
| n |
∴2
| a |
| b |
| a |
| b |
化为(2-λ)
| a |
| b |
| 0 |
∵
| a |
| b |
|
| 1 |
| 2 |
∴当k=-
| 1 |
| 2 |
| m |
| n |
点评:本题考查了数量积的定义及其运算性质、向量垂直与数量积的关系、向量共线定理,考查了计算能力,属于基础题.

练习册系列答案
相关题目
若函数f(x)=ax2+bx+c满足f(4)=f(1),那么( )
| A、f(2)>f(3) |
| B、f(2)=f(3) |
| C、f(2)<f(3) |
| D、无法比较 |

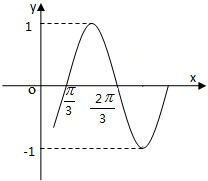 若函数y=Asin(ωx+φ)在平面直角坐标系中的图象(部分)如图所示,其中ω>0,|φ|≤π.
若函数y=Asin(ωx+φ)在平面直角坐标系中的图象(部分)如图所示,其中ω>0,|φ|≤π.