题目内容
11.在直角坐标系xOy中,直线l的参数方程为$\left\{\begin{array}{l}{x=-2+t}\\{y=\sqrt{3}t}\end{array}\right.$(t为参数),若以该直角坐标系的原点O为极点,x轴的非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ+4cosθ=0.(Ⅰ)求直线l与曲线C的普通方程;
(Ⅱ)已知直线l与曲线C交于A,B两点,设M(-2,0),求|$\frac{1}{|MA|}$-$\frac{1}{|MB|}$|的值.
分析 (Ⅰ)由直线l的参数方程消去参数能求出直线l的普通方程;由ρcosθ=x,ρsinθ=y,能求出曲线C的普通方程.
(Ⅱ)设A,B对应的参数为t1,t2,将$\left\{\begin{array}{l}{x=-2+t}\\{y=\sqrt{3}t}\end{array}\right.$代入y2=-4x,得:3t2+4t-8=0,由此利用韦达定理能求出|$\frac{1}{|MA|}$-$\frac{1}{|MB|}$|的值.
解答 解:(Ⅰ)由直线l的参数方程为$\left\{\begin{array}{l}{x=-2+t}\\{y=\sqrt{3}t}\end{array}\right.$(t为参数),得y=$\sqrt{3}$(x-2),
∴直线l的普通方程为$\sqrt{3}x-y-2\sqrt{3}$=0.
由ρsin2θ+4cosθ=0,得ρ2sin2θ+4ρcosθ=0,
又∵ρcosθ=x,ρsinθ=y,∴曲线C的普通方程为y2=-4x.
(Ⅱ)设A,B对应的参数为t1,t2,
将$\left\{\begin{array}{l}{x=-2+t}\\{y=\sqrt{3}t}\end{array}\right.$代入y2=-4x,得:3t2+4t-8=0,
∴${t}_{1}+{t}_{2}=-\frac{4}{3}$,t1t2=-$\frac{8}{3}$,
∵直线l的参数方程为$\left\{\begin{array}{l}{x=-2+t}\\{y=\sqrt{3}t}\end{array}\right.$可化为$\left\{\begin{array}{l}{x=-2+\frac{1}{2}×(2t)}\\{y=\frac{\sqrt{3}}{2}×(2t)}\end{array}\right.$,
∴|MA|=|2t1|,|MB|=|2t2|,∴|$\frac{1}{|MA|}$-$\frac{1}{|MB|}$|=$\frac{|{t}_{1}+{t}_{2}|}{2|{t}_{1}{t}_{2}|}$=$\frac{4}{3}÷\frac{16}{3}$=$\frac{1}{4}$.
点评 本题考查直线、椭圆的直角坐标方程的求法,考查两条线段的倒数差的绝对值的求法,考查极坐标方程、直角坐标方程、参数方程的互化,考查推理论证能力、运算求解能力,考查转化思想、函数与方程思想,是中档题.

| A. | {d|d$≥\frac{3}{10}$} | B. | {d|0$<d<\frac{3}{10}$} | C. | {$\frac{3}{10}$} | D. | {d|d$≥\frac{3}{11}$} |
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |
| A. | (-$\frac{1}{4}$,0) | B. | (0,$\frac{1}{4}$) | C. | ($\frac{1}{4}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,$\frac{3}{4}$) |
| A. | $\frac{4}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{{2\sqrt{13}}}{3}$ | B. | $\frac{{2\sqrt{13}}}{5}$ | C. | $\frac{{\sqrt{13}}}{5}$ | D. | $\frac{{\sqrt{13}}}{3}$ |
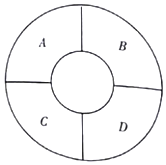 如图,一环形花坛分成A,B,C,D四块,现有3种不同的花供选种,要求在每块里种一种花,且相邻的2块种不同的花,则不同的种法总数为( )
如图,一环形花坛分成A,B,C,D四块,现有3种不同的花供选种,要求在每块里种一种花,且相邻的2块种不同的花,则不同的种法总数为( )