题目内容
已知函数f(x)=
sinxcosx-cos2x+
,x∈R.
(1)求函数f(x)的最小正周期和对称轴;
(2)要得到函数g(x)=sinx的图象,只需将函数f(x)的图象做怎样的变换?
| 3 |
| 1 |
| 2 |
(1)求函数f(x)的最小正周期和对称轴;
(2)要得到函数g(x)=sinx的图象,只需将函数f(x)的图象做怎样的变换?
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)利用二倍角的正弦、余弦函数公式化简f(x)解析式,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,找出ω的值,代入周期公式即可求出f(x)的最小正周期,根据正弦函数的对称性即可确定出对称轴方程;
(2)利用三角函数的图象关系进行变换.
(2)利用三角函数的图象关系进行变换.
解答:
解:(1)f(x)=
sin2x-
cos2x=sin(2x-
),
∵ω=2,
∴f(x)的最小正周期T=
=π,
令2x-
=kπ+
,得到x=
+
(k∈Z),
则图象的对称轴方程为x=
+
(k∈Z);
(2)要得到函数g(x)=sinx的图象,只需将函数f(x)的图象首先向左平移
,得到y=sin2x的图象,然后将y=sin2x的图象上的纵坐标不变,横坐标扩大为原来的2倍.
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∵ω=2,
∴f(x)的最小正周期T=
| 2π |
| 2 |
令2x-
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 3 |
则图象的对称轴方程为x=
| kπ |
| 2 |
| π |
| 3 |
(2)要得到函数g(x)=sinx的图象,只需将函数f(x)的图象首先向左平移
| π |
| 12 |
点评:本题考查了三角函数的恒等变形、三角函数性质的运用以及三角函数图象的变换;属于基础题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
关于方程|log2x|=a(a>0)的两个根x1,x2(x1<x2)以下说法正确的是( )
| A、x1+x2>3 |
| B、x1x2>2 |
| C、x1x2=1 |
| D、1<x1+x2<2 |
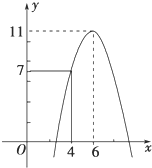 某汽车运输公司购买了一批豪华大客车投入运营.据市场分析,每辆客车营运的总利润y(单位:10万元)与营运年数x(x∈N+)为二次函数的关系(如图),要使营运的年平均利润最大,则每辆客车营运年数为
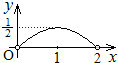
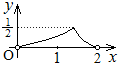
某汽车运输公司购买了一批豪华大客车投入运营.据市场分析,每辆客车营运的总利润y(单位:10万元)与营运年数x(x∈N+)为二次函数的关系(如图),要使营运的年平均利润最大,则每辆客车营运年数为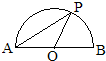 如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x函数关系的图象大致是( )
如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x函数关系的图象大致是( )