题目内容
f(x)=2x4-3x2+1在[
,2]上的最大值、最小值分别是 .
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:先求导数,得y′=8x3-6x,利用导数研究函数的单调性、极值、最值,并列出表格即可得出最大值与最小值.
解答:
解:∵f(x)=2x4-3x2+1,x∈[
,2]
∴f′(x)=8x3-6x=0,
解得x=0或x=
或x=-
(舍去),
∴x∈[
,
)时,f′(x)<0,函数f(x)为减函数;
x∈(
,2]时,f′(x)>0,函数f(x)为增函数;
∴f(x)=2x4-3x2+1在x=
时有最小值,最小值为-
.
又∵f(
)=
,f(2)=21,
∴f(x)的最大值为21.
故答案为21,-
| 1 |
| 2 |
∴f′(x)=8x3-6x=0,
解得x=0或x=
| ||
| 2 |
| ||
| 2 |
∴x∈[
| 1 |
| 2 |
| ||
| 2 |
x∈(
| ||
| 2 |
∴f(x)=2x4-3x2+1在x=
| ||
| 2 |
| 1 |
| 8 |
又∵f(
| 1 |
| 2 |
| 3 |
| 8 |
∴f(x)的最大值为21.
故答案为21,-
| 1 |
| 8 |
点评:熟练掌握利用导数研究函数的单调性、极值、最值的方法是解题的关键.

练习册系列答案
相关题目
设全体实数集为R,M={1,2},N={1,2,3,4},则(∁RM)∩N等于( )
| A、{4} |
| B、{3,4} |
| C、{2,3,4} |
| D、{1,2,3,4} |
 函数f(x)=sin(ωx+φ)(ω>0,|φ|<
函数f(x)=sin(ωx+φ)(ω>0,|φ|<
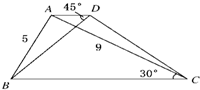 如图所示,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°.则BD的长为
如图所示,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°.则BD的长为