题目内容
在等比数列{an}中,an>0,若a1a2a3…a2012=22012,则a2a2011=( )
| A、2 |
| B、4 |
| C、21005 |
| D、21006 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:根据等比数列的性质,利用等比中项的性质建立方程即可得到结论.
解答:
解:在等比数列{an}中,
∵a1a2012=a2a2011=…=a1006a1007,
∴由a1a2a3…a2012=22012,
得(a2a2011)1006=22012,
即a2a2011=4,
故选:B.
∵a1a2012=a2a2011=…=a1006a1007,
∴由a1a2a3…a2012=22012,
得(a2a2011)1006=22012,
即a2a2011=4,
故选:B.
点评:本题主要考查等比数列项的计算,利用等比数列的性质,结合等比中项的公式是解决本题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
设全体实数集为R,M={1,2},N={1,2,3,4},则(∁RM)∩N等于( )
| A、{4} |
| B、{3,4} |
| C、{2,3,4} |
| D、{1,2,3,4} |
直线l:2xsinα+2ycosα+1=0,圆C:x2+y2+2xsinα+2ycosα=0,l与C的位置关系是( )
| A、相交 | B、相切 |
| C、相离 | D、不能确定 |
设A={-4,2a-1,a2},B={9,a-5,1-a},已知A∩B={9},则实数a的值为( )
| A、5 | B、±3 | C、-3 | D、3 |
cos240°的值为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知A(-2,-2),B(4,2),点P在圆x2+y2=1上运动,则|PA|2+|PB|2的最大值是( )
| A、28 | B、30 | C、32 | D、34 |
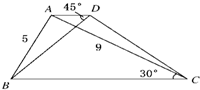 如图所示,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°.则BD的长为
如图所示,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°.则BD的长为