题目内容
12. 如图所示:“十字形”公路的交叉处周围呈扇形形状,某市规划拟在这块扇形土尘修建一个圆形广扬,已知∠A0B=60°,AB的长度=100πm,怎样设计广场的占地面积最大?其值是多少?
如图所示:“十字形”公路的交叉处周围呈扇形形状,某市规划拟在这块扇形土尘修建一个圆形广扬,已知∠A0B=60°,AB的长度=100πm,怎样设计广场的占地面积最大?其值是多少?
分析 由已知及弧长公式可求OA,设⊙O1与OA切于C点,连结O1O、O1C,可得O1C=(300-O1C)×$\frac{1}{2}$,解得O1C,即可求得面积.
解答 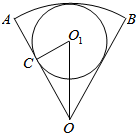 解:如题图,∵∠AOB=60°=$\frac{π}{3}$,$\widehat{AB}$=100π,
解:如题图,∵∠AOB=60°=$\frac{π}{3}$,$\widehat{AB}$=100π,
∴OA=$\frac{100π}{\frac{π}{3}}$=300(m).
欲使圆形广场的占地面积最大,只需⊙O1与扇形相切.
设⊙O1与OA切于C点,连结O1O、O1C,
则∠O1OC=30°=$\frac{π}{6}$,O1O=OA-O1C=300-O1C,
∴O1C=O1Osin$\frac{π}{6}$,即O1C=(300-O1C)×$\frac{1}{2}$.
解得O1C=100(m),这时πO1C2=10 000π(m2).
答:圆形广场的半径为100 m时,其占地面积最大,且最大值为10000π m2.
点评 本题主要考查了弧长公式,圆的面积公式,考查了计算能力,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
7.抛物线y2=3x关于直线y=x对称的抛物线方程为( )
| A. | y2=$\frac{1}{3}$x | B. | x2=3y | C. | x2=$\frac{1}{3}$y | D. | y2=3x |
17.设A是△ABC的一个内角,且sinA=$\frac{\sqrt{3}}{2}$,那么角A等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | kπ+$\frac{π}{3}$(k∈Z) |
 一个几何体的三视图及尺寸如图所示,其中主视图、左视图是等腰三角形,俯视图是圆,则该几何体的表面积为16π.
一个几何体的三视图及尺寸如图所示,其中主视图、左视图是等腰三角形,俯视图是圆,则该几何体的表面积为16π.