题目内容
18.如图是一个几何体的三视图,其俯视图是边长为3的正三角形,则该几何体的表面积为( )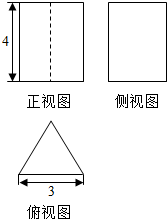
| A. | 36 | B. | 36$+\frac{9\sqrt{3}}{4}$ | C. | 36$+\frac{9\sqrt{3}}{2}$ | D. | 18$+\frac{9\sqrt{3}}{2}$ |
分析 已知中的三视图可得:该几何体是一个以俯视图为底面的三棱柱,根据柱体表面积公式,可得答案.
解答 解:已知中的三视图可得:该几何体是一个以俯视图为底面的三棱柱,
其底面边长为3,
故底面面积为:$\frac{\sqrt{3}}{4}•{3}^{2}$=$\frac{9\sqrt{3}}{4}$,
底面周长C=9,
高h=4,
故侧面积为:4×9=36,
故柱体的表面积S=36+2×$\frac{9\sqrt{3}}{4}$=36+$\frac{9\sqrt{3}}{2}$,
故选:C
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
9.若l,m,n是不相同的空间直线,α,β是不重合的两个平面,则下列命题正确的是( )
| A. | l⊥α,m⊥β,l⊥m⇒α⊥β | B. | l∥m,m⊆α⇒l∥α | ||
| C. | l⊆α,m⊆α,l∥β,m∥β⇒α∥β | D. | l⊥n,m⊥n⇒l∥m |
13.已知命题p:?x∈R,|x|<0,则¬p是( )
| A. | ?x∈R,|x|≥0 | B. | ?x∈R,|x|>0 | C. | ?x∈R,|x|≥0 | D. | ?x∈R,|x|<0 |
8.已知某几何体的三视图如上图所示,则该几何体的体积为( )
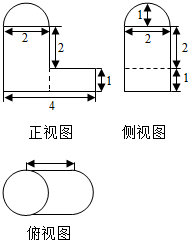

| A. | 3+$\frac{10}{3}$π | B. | 4+$\frac{11}{3}$π | C. | 3+$\frac{11}{3}$π | D. | 4+$\frac{8}{3}$π |
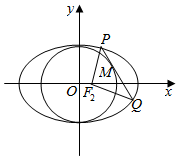 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点H(3,0)在椭圆上
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点H(3,0)在椭圆上