题目内容
19．已知等比数列{an}前n项和满足Sn=1-A•3n，数列{bn}是递增数列，且bn=An2+Bn，则A=1，B的取值范围为（-3，+∞）．分析 由等比数列{an}前n项和满足Sn=1-A•3n，分别求出前三项，利用等比数列{an}中${{a}_{2}}^{2}={a}_{1}{a}_{3}$，能求出A．根据数列{bn}是递增数列，且bn=An2+Bn=n2+Bn，利用bn+1-bn＞0，能求出B的取值范围．
解答 解：∵等比数列{an}前n项和满足Sn=1-A•3n，
∴a1=S1=1-3A，
a2=S2-S1=（1-9A）-（1-3A）=-6A，
a3=S3-S2=（1-27A）-（1-9A）=-18A，
∵等比数列{an}中${{a}_{2}}^{2}={a}_{1}{a}_{3}$，
∴36A2=（1-3A）（-18A），
解得A=1或A=0（舍），故A=1．
∵数列{bn}是递增数列，且bn=An2+Bn=n2+Bn，
∴bn+1-bn=（n+1）2+B（n+1）-（n2+Bn）=2n+1+B＞0．
∴B＞-2n-1，
∵n∈N*，∴B＞-3．
∴B的取值范围为（-3，+∞）．
故答案为：1，（-3，+∞）．
点评 本题考查实数值的求法，考查实数的取值范围的求法，是基础题，解题时要认真审题，注意等比数列的性质、递增数列的性质的合理运用．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
10．已知x∈R，符号[x]表示不超过x的最大整数，如[1.9]=1，[2.01]=2．若函数$f（x）=\frac{x}{[x]}-m$（x≥1）有且仅有三个零点，则m的取值范围是（ ）
| A． | $[{\frac{3}{2}，2}]$ | B． | $[{\frac{3}{2}，2}）$ | C． | $[{\frac{5}{4}，\frac{4}{3}}）$ | D． | $[{\frac{5}{4}，\frac{4}{3}}]$ |
7．已知函数$f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜\frac{π}{2}）$一个周期的图象如图所示，则φ的值为（ ）
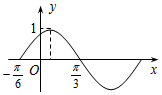
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{3π}{8}$ |
14．在复平面内，已知复数z=$\frac{|1-i|+2i}{1-i}$，则z在复平面上对应的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
11．已知经过M（-2，m），N（m，4）的直线的斜率等于1，则m的值为（ ）
| A． | 1 | B． | 3 | C． | 4 | D． | 3或4 |