题目内容
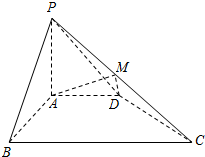 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形AB⊥CD,BC∥AD且BC=4,点M为PC中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形AB⊥CD,BC∥AD且BC=4,点M为PC中点.(1)求证:平面ADM⊥平面PBC;
(2)求点P到平面ADM的距离.
考点:点、线、面间的距离计算,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)取PB中点N,连结MN、AN,证明四边形ADMN为平行四边形,AN⊥平面PBC,可得平面ADM⊥平面PBC;
(2)PN⊥平面ADM,即点P到平面ADM的距离为PN,即可求点P到平面ADM的距离.
(2)PN⊥平面ADM,即点P到平面ADM的距离为PN,即可求点P到平面ADM的距离.
解答:
 解:(1)取PB中点N,连结MN、AN,则
解:(1)取PB中点N,连结MN、AN,则
∵M是PC中点,∴MN∥BC,MN=
BC=2,
又∵BC∥AD,∴MN∥AD,MN=AD,
∴四边形ADMN为平行四边形,
∵AP⊥AD,AB⊥AD,∴AD⊥平面PAB,
∴AD⊥AN,∴AN⊥MN,
∵AP=AB,∴AN⊥PB,∴AN⊥平面PBC,
∵AN?平面ADM,
∴平面ADM⊥平面PBC.
(2)由(1)知,PN⊥AN,PN⊥AD,
∴PN⊥平面ADM,即点P到平面ADM的距离为PN,
在Rt△PAB中,由PA=AB=2,得PB=2
,
∴PN=
PB=
.
 解:(1)取PB中点N,连结MN、AN,则
解:(1)取PB中点N,连结MN、AN,则∵M是PC中点,∴MN∥BC,MN=
| 1 |
| 2 |
又∵BC∥AD,∴MN∥AD,MN=AD,
∴四边形ADMN为平行四边形,
∵AP⊥AD,AB⊥AD,∴AD⊥平面PAB,
∴AD⊥AN,∴AN⊥MN,
∵AP=AB,∴AN⊥PB,∴AN⊥平面PBC,
∵AN?平面ADM,
∴平面ADM⊥平面PBC.
(2)由(1)知,PN⊥AN,PN⊥AD,
∴PN⊥平面ADM,即点P到平面ADM的距离为PN,
在Rt△PAB中,由PA=AB=2,得PB=2
| 2 |
∴PN=
| 1 |
| 2 |
| 2 |
点评:本小题主要考查立体几何的相关知识,具体涉及到线面以及面面的垂直关系、点到平面的距离等问题.

练习册系列答案
相关题目
若y=ax2+bx+c(a<0)中,两个零点x1<0,x2>0,且x1+x2>0,则( )
| A、b>0,c>0 |
| B、b>0,c<0 |
| C、b<0,c>0 |
| D、b<0,c<0 |
在正方体ABCD-A1B1C1D1中,动点P在底面ABCD内,且P到棱AD的距离与到面对角线BC1的距离相等,则点P的轨迹是( )
| A、线段 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
 在如图所示的几何体中,四边形ABCD和ABEF均为矩形,M为AF的中点,BN⊥CE与N.
在如图所示的几何体中,四边形ABCD和ABEF均为矩形,M为AF的中点,BN⊥CE与N.