题目内容
解方程:log2(2x+
)•log2(2x+1+
)=2.
| ||
| 2 |
| 2 |
考点:指、对数不等式的解法
专题:函数的性质及应用
分析:利用t=log2(2x+
),换元法,求几位方程的解,然后利用指数方程求解即可.
| ||
| 2 |
解答:
解:令t=log2(2x+
),
则log2(2x+
)•log2(2x+1+
)=2.
即log2(2x+
)•(1+log2(2x+
))=2.
化为:t(t+1)=2,
即t2+t-2=0,解得t=1,或t=-2,
log2(2x+
)=1时,可得2x+
=2,解得x=log2(4-
)-1.
log2(2x+
)=-2时,可得2x+
=2-2,解得x∈∅.
方程的解为:x=log2(4-
)-1.
| ||
| 2 |
则log2(2x+
| ||
| 2 |
| 2 |
即log2(2x+
| ||
| 2 |
| ||
| 2 |
化为:t(t+1)=2,
即t2+t-2=0,解得t=1,或t=-2,
log2(2x+
| ||
| 2 |
| ||
| 2 |
| 2 |
log2(2x+
| ||
| 2 |
| ||
| 2 |
方程的解为:x=log2(4-
| 2 |
点评:本题考查指数与对数方程的解法,换元法的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=2x3-6x的“临界点”是( )
| A、1 | B、-1 | C、-1和1 | D、0 |
如图,在△OAB中,P为线段AB上的一点,
=x
+y
,且
=3
,则( )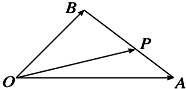
| OP |
| OA |
| OB |
| BP |
| PA |

A、x=
| ||||
B、x=
| ||||
C、x=
| ||||
D、x=
|
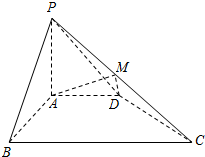 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形AB⊥CD,BC∥AD且BC=4,点M为PC中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形AB⊥CD,BC∥AD且BC=4,点M为PC中点.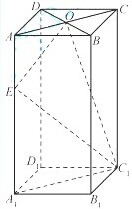 如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,E为棱AA1上任意一点,F是CD的中点.
如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,E为棱AA1上任意一点,F是CD的中点.