题目内容
在如图所示的几何体中，四边形ABCD和ABEF均为矩形，M为AF的中点，BN⊥CE与N．（1）求证：CF∥平面MBD；
（2）求证：平面EFC⊥平面BDN．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（Ⅰ）连接AC交BD于点O，连接OM，由三角形中位线定理得CF∥OM，由此能证明CF∥平面MBD．
（Ⅱ）由四边形ABCD和ABEF均为矩形，得AB⊥平面BCE，从而BN⊥面EFC，由此能证明平面EFC⊥平面BDN．
（Ⅱ）由四边形ABCD和ABEF均为矩形，得AB⊥平面BCE，从而BN⊥面EFC，由此能证明平面EFC⊥平面BDN．
解答：
证明：（Ⅰ）连接AC交BD于点O，连接OM．
因为四边形ABCD是正方形，所以O为AC的中点．
因为M为AF的中点，所以CF∥OM，
又OM?平面MBD，CF?平面MBD，
所以CF∥平面MBD．（6分）
（Ⅱ）因为四边形ABCD和ABEF均为矩形，
所以AB⊥平面BCE，
所以AB⊥BN，又AB∥EF，所以BN⊥EF，
又BN⊥EC（已知），
所以BN⊥面EFC，
又BN?平面BDN，所以平面EFC⊥平面BDN．（12分）
因为四边形ABCD是正方形，所以O为AC的中点．
因为M为AF的中点，所以CF∥OM，
又OM?平面MBD，CF?平面MBD，
所以CF∥平面MBD．（6分）
（Ⅱ）因为四边形ABCD和ABEF均为矩形，
所以AB⊥平面BCE，
所以AB⊥BN，又AB∥EF，所以BN⊥EF，
又BN⊥EC（已知），
所以BN⊥面EFC，
又BN?平面BDN，所以平面EFC⊥平面BDN．（12分）
点评：本题考查线面平行的证明，考查面面垂直的证明，考查方程思想、等价转化思想等数学思想方法和学生的空间想象能力、逻辑推理能力和运算求解能力，是中档题．
练习册系列答案
相关题目
| 3 | a |
| 3 | b |
| 3 | a-b |
| A、ab（b-a）＞0 |
| B、ab＞0且a＞b |
| C、ab＜0且a＜b |
| D、ab（b-a）＜0 |
已知过定点P（2，0）的直线l与曲线y=
相交于A，B两点，O为坐标原点，当S△AOB=1时，直线l的倾斜角为（ ）
| 2-x2 |
| A、150° | B、135° |
| C、120° | D、不存在 |
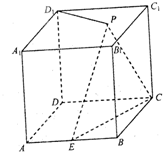在棱长为2的正方体ABCD-A1B1C1D1中，E为棱AB的中点，点P在平面A1B1C1D1内，若D1P⊥平面PCE，试求线段D1P的长．
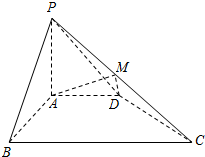如图，在四棱锥P-ABCD中，PA⊥平面ABCD，PA=AB=AD=2，四边形AB⊥CD，BC∥AD且BC=4，点M为PC中点．