题目内容
设函数f（x）=x+
（0≤x≤2），若当x=0时函数值最大，则实数a的取值范围是（ ）
| a |
| x+1 |
| A、a≥1 | B、a≤1 |
| C、a≥3 | D、a≤3 |
考点：函数的最值及其几何意义
专题：计算题,函数的性质及应用
分析：根据条件确定f（0）≥f（2），可得a≥2+
，即可求出实数a的取值范围．
| a |
| 3 |
解答：
解：设x+1=t，则1≤t≤3，
∴y=t+
-1，
∴y′=1-
，
∵当x=0时函数值最大，
∴当t=1时函数值最大，
∴f（0）≥f（2），
∴a≥2+
，
∴a≥3，
故选：C．
∴y=t+
| a |
| t |
∴y′=1-
| a |
| t2 |
∵当x=0时函数值最大，
∴当t=1时函数值最大，
∴f（0）≥f（2），
∴a≥2+
| a |
| 3 |
∴a≥3，
故选：C．
点评：本题考查实数a的取值范围，考查学生的计算能力，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=ln（x+1）•tanx的图象可能是（ ）
A、 |
B、 |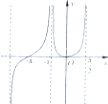
C、 |
D、 |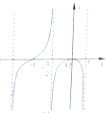
函数f（x）=sin（x+
）在（0，2π）上的图象与x轴的交点的横坐标为（ ）
| π |
| 6 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
十进制数（6）10 转化成二进制数为（ ）
| A、（100）2 |
| B、（101）2 |
| C、（111）2 |
| D、（110）2 |
i为虚数单位，若a=
，则a的值为（ ）
| 5 |
| i-2 |
| A、2+i | B、2-i |
| C、-2-i | D、-2+i |
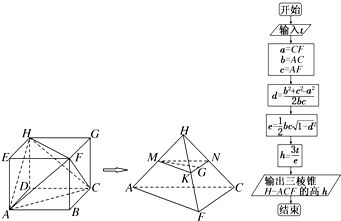
阅读如图的程序框图，运行相应的程序，输出的结果为（ ）
A、-
| ||
B、
| ||
| C、3 | ||
D、
|