题目内容
某工厂欲加工一件艺术品,需要用到三棱锥形状的坯材,工人将如图所示的长方体ABCDEFGH材料切割成三棱锥HACF.
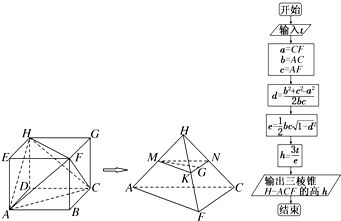
(1)若点M,N,K分别是棱HA,HC,HF的中点,点G是NK上的任意一点,求证:MG∥平面ACF;
(2)已知原长方体材料中,AB=2m,AD=3m,DH=1m,根据艺术品加工需要,工程师必须求出该三棱锥的高.工程师设计了一个求三棱锥的高度的程序,其框图如图所示,则运行该程序时乙工程师应输入的t的值是多少?

(1)若点M,N,K分别是棱HA,HC,HF的中点,点G是NK上的任意一点,求证:MG∥平面ACF;
(2)已知原长方体材料中,AB=2m,AD=3m,DH=1m,根据艺术品加工需要,工程师必须求出该三棱锥的高.工程师设计了一个求三棱锥的高度的程序,其框图如图所示,则运行该程序时乙工程师应输入的t的值是多少?
考点:程序框图,直线与平面平行的判定
专题:应用题,空间位置关系与距离,算法和程序框图
分析:(1)由已知及直线与平面平行的判定先证明MK∥平面ACF,同理可证MN∥平面ACF,可证平面MNK∥平面ACF,由面面平行的性质即可证明MG∥平面ACF.
(2)由程序框图可知a=CF,b=AC,c=AF,依次可求d,e,又h=
,可得t=
he=V三棱锥HACF.由三棱锥HACF为将长方体ABCDEFGH切掉4个体积相等的小三棱锥所得,即可求t的值.
(2)由程序框图可知a=CF,b=AC,c=AF,依次可求d,e,又h=
| 3t |
| e |
| 1 |
| 3 |
解答:
解:(1)证明:∵HM=MA,HN=NC,HK=KF,
∴MK∥AF,MN∥AC.
∵MK?平面ACF,AF?平面ACF,
∴MK∥平面ACF,
同理可证MN∥平面ACF,
∵MN,MK?平面MNK,且MK∩MN=M,
∴平面MNK∥平面ACF,又MG?平面MNK,故MG∥平面ACF.
(2)由程序框图可知a=CF,b=AC,c=AF,
∴d=
=
=cos∠CAF,
∴e=
bc
=
AC•AF•sin∠CAF=S△ACF.
又h=
,∴t=
he=
h•S△ACF=V三棱锥HACF.
∵三棱锥HACF为将长方体ABCDEFGH切掉4个体积相等的小三棱锥所得,
∴V三棱锥HACF=2×3×1-4×
×
×3×2×1=6-4=2,
故t=2.
∴MK∥AF,MN∥AC.
∵MK?平面ACF,AF?平面ACF,
∴MK∥平面ACF,
同理可证MN∥平面ACF,
∵MN,MK?平面MNK,且MK∩MN=M,
∴平面MNK∥平面ACF,又MG?平面MNK,故MG∥平面ACF.
(2)由程序框图可知a=CF,b=AC,c=AF,
∴d=
| b2+c2-a2 |
| 2bc |
| AC2+AF2-CF2 |
| 2AC•AF |
∴e=
| 1 |
| 2 |
| 1-d2 |
| 1 |
| 2 |
又h=
| 3t |
| e |
| 1 |
| 3 |
| 1 |
| 3 |
∵三棱锥HACF为将长方体ABCDEFGH切掉4个体积相等的小三棱锥所得,
∴V三棱锥HACF=2×3×1-4×
| 1 |
| 3 |
| 1 |
| 2 |
故t=2.
点评:本题主要考查了直线与平面平行的判定,面面平行的性质,程序框图和算法的应用,综合性较强,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
一个正八面体的八个顶点都在同一个球面上,如果该正八面体的棱长为
.则这个球的表面积为( )
| 2 |
| A、π | ||
| B、2π | ||
| C、4π | ||
D、
|
已知x∈(0,1)时,函数f(x)=
的最小值为b,若定义在R上的函数g(x)满足:对任意m,n∈R都有g(m+n)=g(m)+g(n)+b,则下列结论正确的是( )
| 1+2x2 | ||
2x
|
| A、g(x)-1是奇函数 | ||
| B、g(x)+1是奇函数 | ||
C、g(x)-
| ||
D、g(x)-
|
设函数f(x)=x+
(0≤x≤2),若当x=0时函数值最大,则实数a的取值范围是( )
| a |
| x+1 |
| A、a≥1 | B、a≤1 |
| C、a≥3 | D、a≤3 |
已知圆O:x2+y2=5和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积为( )
| A、5 | ||
| B、10 | ||
C、
| ||
D、
|
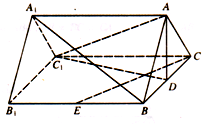 如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形.