题目内容
已知集合P={x|f（x）=0}，Q={x|g（x）=0}，则集合M={x|f（x）g（x）=0}可表示为（ ）
| A、P | B、P∪Q |
| C、P∩Q | D、以上答案都不对 |
考点：并集及其运算
专题：集合
分析：由f（x）g（x）=0等价于
，得到集合M={x|f（x）g（x）=0}是{x|f（x）=0}和{x|g（x）=0}的交集．
|
解答：
解：∵f（x）g（x）=0，
∴
，
∵集合P={x|f（x）=0}，Q={x|g（x）=0}，
∴集合M={x|f（x）g（x）=0}可表示为P∩Q．
故选：C．
∴
|
∵集合P={x|f（x）=0}，Q={x|g（x）=0}，
∴集合M={x|f（x）g（x）=0}可表示为P∩Q．
故选：C．
点评：本题考查集合的求法，是基础题，解题时要注意函数性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
欧阳修《卖油翁》中写到：（翁）乃取一葫芦置于地，以钱覆其口，徐以杓酌油沥之，自钱孔入，而钱不湿．可见“行行出状元”，卖油翁的技艺让人叹为观止．若铜钱是直径为3cm的圆，中间有边长为1cm的正方形孔，若你随机向铜钱上滴一滴油，则油（油滴的大小忽略不计）正好落入孔中的概率（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f（x）=loga（4-ax）在[-1，2]上单调递减，则正实数a的取值范围是（ ）
| A、a＞2 | ||
| B、1＜a＜2 | ||
C、
| ||
| D、以上都不对 |
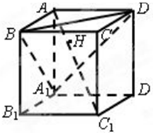如图，正方体AC1的棱长为1，连结AC1，交平面A1BD于H，有以下四个命题：