题目内容
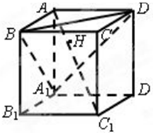 如图,正方体AC1的棱长为1,连结AC1,交平面A1BD于H,有以下四个命题:
如图,正方体AC1的棱长为1,连结AC1,交平面A1BD于H,有以下四个命题:①AC1⊥平面A1BD,
②H是△A1BD的垂心,
③AH=
| ||
| 3 |
④直线AH和BB1所成的角为45°.
则上述命题中,是真命题的有
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①由正方体的性质可得:AC1⊥BD,AC1⊥A1B,利用线面垂直的判定定理即可得出;
②H是等边△A1BD的中心,可得H是△A1BD的垂心;
③由VA-BDA1=VA1-ABD即可得出AH=
;
④直线AH即AC1和BB1(即AA1)所成的角θ满足:tanθ=
,即可判断出.
②H是等边△A1BD的中心,可得H是△A1BD的垂心;
③由VA-BDA1=VA1-ABD即可得出AH=
| ||
| 3 |
④直线AH即AC1和BB1(即AA1)所成的角θ满足:tanθ=
| 2 |
解答:
解:①由正方体的性质可得:AC1⊥BD,AC1⊥A1B,而BD∩A1B=B,∴AC1⊥平面A1BD,正确;
②H是等边△A1BD的中心,因此是△A1BD的垂心,正确;
③由VA-BDA1=VA1-ABD,∴
•AH•
×(
)2=
×
×12×1,解得AH=
,正确;
④直线AH即AC1和BB1(即AA1)所成的角θ满足:tanθ=
,因此不是45°,不正确.
综上可得:只有①②③正确.
故答案为:①②③.
②H是等边△A1BD的中心,因此是△A1BD的垂心,正确;
③由VA-BDA1=VA1-ABD,∴
| 1 |
| 3 |
| ||
| 4 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
④直线AH即AC1和BB1(即AA1)所成的角θ满足:tanθ=
| 2 |
综上可得:只有①②③正确.
故答案为:①②③.
点评:本题考查了正方体的对角线的性质、三棱锥的体积计算公式、异面直线所成的角、等边三角形的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知集合P={x|f(x)=0},Q={x|g(x)=0},则集合M={x|f(x)g(x)=0}可表示为( )
| A、P | B、P∪Q |
| C、P∩Q | D、以上答案都不对 |
下列各函数中,其图象经过点(1,0)的是( )
| A、y=x2+1 | ||
B、y=
| ||
| C、y=3x | ||
| D、y=log2x |
 设函数y=2sinx(0≤x≤п)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)单调递增区间
设函数y=2sinx(0≤x≤п)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)单调递增区间