题目内容
欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为3cm的圆,中间有边长为1cm的正方形孔,若你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:应用题,空间位置关系与距离
分析:求出铜钱面积的大小和中间正方形孔面积的大小,然后代入几何概型计算公式进行求解.
解答:
 解:如图所示:
解:如图所示:
∵S正=1,S圆=π•(
)2=
∴P=
=
故选:A
 解:如图所示:
解:如图所示:∵S正=1,S圆=π•(
| 3 |
| 2 |
| 9π |
| 4 |
∴P=
| S正方形 |
| S圆 |
| 4 |
| 9π |
故选:A
点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据几何概率的公式求解.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
已知直线l1:2y=x+2与直线l2:y+2x+1=0,则l1与l2的位置关系为( )
| A、相交不垂直 | B、相交且垂直 |
| C、平行不重合 | D、重合 |
在复平面内,复数z=
(i为虚数单位)对应的点位于( )
| 2+4i |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
图中阴影部分表示的集合是( )


| A、∁U(A∩B) |
| B、∁U(A∪B) |
| C、A∩(∁UB) |
| D、(∁UA)∩B |
在复平面内,复数Z=
+i2012对应的点位于( )
| 2 |
| 3-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合P={x|f(x)=0},Q={x|g(x)=0},则集合M={x|f(x)g(x)=0}可表示为( )
| A、P | B、P∪Q |
| C、P∩Q | D、以上答案都不对 |
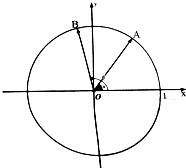 如图所示,在平面直角坐标系中,锐角α和钝角β的终边分别于单位圆交于A,B两点,
如图所示,在平面直角坐标系中,锐角α和钝角β的终边分别于单位圆交于A,B两点,