题目内容
 将圆x2+y2=4上点的横坐标保持不变,纵坐标变为原来的一半,所得曲线设为E.
将圆x2+y2=4上点的横坐标保持不变,纵坐标变为原来的一半,所得曲线设为E.(1)求曲线E的方程;
(2)若曲线E与x轴、y轴分别交于点A(a,0),B(-a,0),C(0,b),其中a>0,b>0.过点C的直线l与曲线E交于另一点D,并与x轴交于点P,直线AC与直线BD交于点Q.当点P异于点B时,求证:
| OP |
| OQ |
考点:直线和圆的方程的应用
专题:圆锥曲线中的最值与范围问题
分析:(1)在曲线C上任取一个动点P(x,y),根据图象的变换可知点( x,2y)在圆x2+y2=4上,由此能求出曲线E的方程.
(2)根据题意可设直线l的方程为y=kx+1,由
,得(4k2+1)x2+8kx=0.由此利用已知条件能证明
•
为定值4.
(2)根据题意可设直线l的方程为y=kx+1,由
|
| OP |
| OQ |
解答:
(本题满分10分)
解:(1)在曲线C上任取一个动点P(x,y),
根据图象的变换可知点( x,2y)在圆x2+y2=4上,
∴x2+4y2=4,
∴曲线E的方程为
+y2=1.(说明:没有过程得2分) …(4分)
(2)根据题意可设直线l的方程为y=kx+1,
由
可得(4k2+1)x2+8kx=0.
解得x=0或x=
,代入直线l方程得D点坐标为(
,
).…(6分)
又直线AC的方程为
+y=1,直线BD的方程为y=
(x+2),
联立
…(8分)
解得
因此Q(-4k,2k+1),又P(-
,0),
所以
•
=(-
,0)•(-4k,2k+1)=4.
故
•
为定值4.…(10分)
解:(1)在曲线C上任取一个动点P(x,y),
根据图象的变换可知点( x,2y)在圆x2+y2=4上,
∴x2+4y2=4,
∴曲线E的方程为
| x2 |
| 4 |
(2)根据题意可设直线l的方程为y=kx+1,
由
|
解得x=0或x=
| -8k |
| 4k2+1 |
| -8k |
| 4k2+1 |
| 1-4k2 |
| 4k2+1 |
又直线AC的方程为
| x |
| 2 |
| 1+2k |
| 2-4k |
联立
|
解得
|
因此Q(-4k,2k+1),又P(-
| 1 |
| k |
所以
| OP |
| OQ |
| 1 |
| k |
故
| OP |
| OQ |
点评:本题考查曲线E的方程的求法,考查
•
为定值的证明,解题时要认真审题,注意函数与方程思想的合理运用.
| OP |
| OQ |

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
以下现象是随机现象的是( )
| A、标准大气压下,水加热到100℃,必会沸腾 |
| B、走到十字路口,遇到红灯 |
| C、长和宽分别为a、b的矩形,其面积为a×b |
| D、实系数一次方程必有一实根 |
已知正方形ABCD的边长为2,E为CD的中点,F为AD的中点,则
•
=( )
| AE |
| BF |
| A、0 | B、1 | C、2 | D、4 |
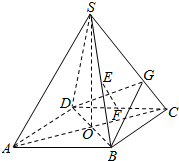 正四棱锥S-ABCD中,O为底面中心,SO=AB=2,E、F分别为SB、CD的中点.
正四棱锥S-ABCD中,O为底面中心,SO=AB=2,E、F分别为SB、CD的中点.