Question

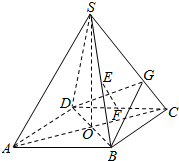正四棱锥S-ABCD中，O为底面中心，SO=AB=2，E、F分别为SB、CD的中点．
（1）求证：EF∥平面SAD；
（2）若G为SC上一点，且SG：GC=2：1，求证：SC⊥平面GBD．

Answer 1

考点：直线与平面垂直的判定,直线与平面平行的判定

专题：证明题,空间位置关系与距离

分析：（1）取SA的中点M，连接EM、DM，可证四边形EFDM为平行四边形，即可证明EF∥平面SAD；
（2）先证明SC⊥BD，在OC上取点H，使得OH：HC=2：1，连接GH、OG，可得SO，OG，SG的值，从而由SG²+OG²=

24

9

+

12

9

=4=SO²可证SG⊥OG，即SC⊥OG，又SC⊥BD，从而得证．

解答： 证明：（1）取SA的中点M，连接EM、DM，在△SAB中，EN

∥

.

1

2

AB，又DF

∥

.

1

2

AB，
∴EM

∥

.

DF，
∴四边形EFDM为平行四边形
∴EF∥DM，又EF?平面SAD，DM?平面SAD
∴EF∥平面SAD．

（2）∵SO⊥地面ABCD，BD?平面ABCD
∴SO⊥BD，又BD⊥AC，SO∩AC=O，SO，AC?平面SAC
∴BD⊥平面SAC，SC?平面SAC
∴SC⊥BD
在OC上取点H，使得OH：HC=2：1，连接GH、OG，
∵

SG

GC

=

OH

HC

，∴GH∥SO∴GH⊥OC
Rt△GHO中，OH=

2

3

OC=

2 2

3

，GH=

1

3

SO=

2

3

∴OG=

OH2+GH2

=

8 9 + 4 9

=

2 3

3

Rt△SOC中，SC=

SO2+OC2

=

4+2

=

6

，∴SG=

2 6

3

，
△SOG中，SG²+OG²=

24

9

+

12

9

=4=SO²
∴SG⊥OG，即SC⊥OG，又SC⊥BD，OG、BD?平面GBD，OG∩BD=O
∴SC⊥平面GBD．

点评：本题主要考察了直线与平面垂直的判定，直线与平面平行的判定，考查了转化思想，属于中档题．