题目内容
10.已知抛物线C:y2=2px(p>0)的焦点为F,且经过点A(1,2),过点F的直线与抛物线C交于P,Q两点.(Ⅰ)求抛物线C的方程;
(Ⅱ)O为坐标原点,直线OP,OQ与直线x=-$\frac{p}{2}$分别交于S,T两点,试判断$\overrightarrow{FS}$•$\overrightarrow{FT}$是否为定值?若是,求出这个定值;若不是,请说明理由.
分析 (Ⅰ)把点A(1,2)代入抛物线C的方程,解得p=2,即可求出抛物线方程.
(Ⅱ)求出抛物线的准线方程x=-1,焦点F的坐标为(1,0),设出直线PQ的方程为x=ty+1,求出PQ坐标,求出直线OP的方程,直线OQ的方程,然后求出S,T的坐标,联立直线与抛物线方程,通过韦达定理,结合$\overrightarrow{FS}•\overrightarrow{FT}$化简求解即可.
解答 (本小题共13分)
解:(Ⅰ)把点A(1,2)代入抛物线C的方程y2=2px,得4=2p,解得p=2,
所以抛物线C的方程为y2=4x.….(4分)
(Ⅱ)因为p=2,所以直线$x=-\frac{p}{2}$为x=-1,焦点F的坐标为(1,0)
设直线PQ的方程为x=ty+1,$P(\frac{{{y_1}^2}}{4},{y_1})$,$Q(\frac{{{y_2}^2}}{4},{y_2})$,
则直线OP的方程为$y=\frac{4}{y_1}x$,直线OQ的方程为$y=\frac{4}{y_2}x$.….(5分)
由$\left\{\begin{array}{l}y=\frac{4}{y_1}x\\ x=-1\end{array}\right.$得$S(-1,-\frac{4}{y_1})$,同理得$T(-1,-\frac{4}{y_2})$. ….(7分)
所以$\overrightarrow{FS}=(-2,-\frac{4}{y_1})$,$\overrightarrow{FT}=(-2,-\frac{4}{y_2})$,则$\overrightarrow{FS}•\overrightarrow{FT}=4+\frac{16}{{{y_1}{y_2}}}$. ….(9分)
由$\left\{\begin{array}{l}x=ty+1\\{y^2}=4x\end{array}\right.$得y2-4ty-4=0,所以y1y2=-4,….(11分)
则$\overrightarrow{FS}•\overrightarrow{FT}=4+\frac{16}{(-4)}$=4-4=0.
所以,$\overrightarrow{FS}•\overrightarrow{FT}$的值是定值,且定值为0.….(13分)
点评 本题考查抛物线的简单性质以及抛物线方程的求法,直线与抛物线的位置关系的应用,考查转化思想以及计算能力.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
表1:男生身高频数分布表
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 13 | 13 | 5 | 2 |
| 身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 8 | 12 | 5 | 3 | 1 |
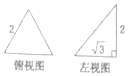 已知三棱锥的俯视图与左视图如图所示,俯视图是边长为2的正三角形,左视图是有一条直角边为2的直角三角形,则该三棱锥的主视图可能为( )
已知三棱锥的俯视图与左视图如图所示,俯视图是边长为2的正三角形,左视图是有一条直角边为2的直角三角形,则该三棱锥的主视图可能为( )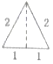

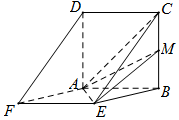 已知边长为2的正方形ABCD与菱形ABEF所在平面互相垂直,M为BC中点.
已知边长为2的正方形ABCD与菱形ABEF所在平面互相垂直,M为BC中点.