题目内容

已知点A是圆ρ=2cosθ的圆心，则点A到直线ρcosθ+
3
ρsinθ=7的距离是
 
．
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：把圆、直线的极坐标方程化为直角坐标方程，利用点到直线的距离公式求得点A到直线的距离．
解答： 解：圆ρ=2cosθ即 （x-1）2+y2=1，它的圆心为A（1，0），
直线ρcosθ+
3
ρsinθ=7 即 x+
3
y-7=0，点A到直线的距离为
|1+0-7|
1+3
=3，
故答案为：3．
点评：本题主要考查把极坐标方程化为直角坐标方程的方法，点到直线的距离公式的应用，属于基础题．
练习册系列答案
相关题目
如图，已知F1、F2为椭圆
x2
2
+y2=1的两焦点，M是椭圆上一点，延长F1M到N，P是NF2上一点，且满足
F2N
=2
F2P
，
MP
•
F2N
=0，点N的轨迹为E．
（1）求曲线E的方程；
（2）过F1的直线l交椭圆于G，交于曲线E于H，（G、H都在x轴的上方），若
F1H
=2
F1G
，求直线l的方程．
设a是一个自然数，f（a）是a的各位数字的平方和，定义数列{an}：a1是自然数，an=f（an-1）（n∈N*，n≥2）．
（Ⅰ）求f（99），f（2014）；
（Ⅱ）若a1≥100，求证：a1＞a2；
（Ⅲ）当a1＜1000时，求证：存在m∈N*，使得a3m=a2m．
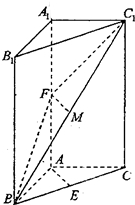如图，在三棱柱ABC-A1B1C1中，A1A⊥面ABC，∠BAC=90°，E为BC的中点，F为A1A的中点，A1A=4，AB=AC=2．
（Ⅰ）求证AE⊥平面 BCC1；
（Ⅱ）求证AE∥平面BFC1；
（Ⅲ）在棱AA1上是否存在点P，使得二面角B-PC1-C的大小是45°，若存在，求出AP的长．若不存在，请说明理由．
圆C：ρ=2sinθ的圆心到直线l：ρsinθ=-2的距离为
 
．
平面α截半径为2的球O所得的截面圆的面积为π，则球心O到平面α的距离为
 
．
若f（x）是定义在[-1，1]上的减函数，则不等式f（x）-f（4x+1）＞0的解集是
 
．
已知正方体ABCD-A1B1C1D1的各棱长为2，则D1到面AB1C的距离为
 
．
函数f（x）=3x-x3的单调递增区间是（　　）
A、[-1，1]
B、[1，+∞）∪（-∞，-1]
C、[1，+∞）及（-∞，-1]
D、[-
3
，
3
]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网