题目内容
已知数列{an}的前n项和为Sn,满足Sn=2an-2,数列{bn}满足{bn}=log2an.
(1)求数列{an}和{bn}的通项公式;
(2)记{
}的前n项和为Tn,求Tn;
(3)若不等式λ2-
λ>Tn对任意n∈N*恒成立,求λ的取值范围.
(1)求数列{an}和{bn}的通项公式;
(2)记{
| 1 |
| bn•bn+1 |
(3)若不等式λ2-
| 3 |
| 2 |
考点:数列的求和,数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由已知条件推导出an=2an-1,从而得到an=2•2n-1=2n.bn=log2an=log22n=n.
(2)由
=
=
-
,利用裂项求和法能求出{
}的前n项和为Tn.
(3)Tn=1-
>1,由此得到λ2-
λ>1,从而能求出λ的取值范围.
(2)由
| 1 |
| bnbn+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| bn•bn+1 |
(3)Tn=1-
| 1 |
| n+1 |
| 3 |
| 2 |
解答:
解:(1)∵Sn=2an-2,
∴n=1时,a1=S1=2a1-2,解得a1=2.
n≥2时,an=Sn-Sn-1=2an-2-(2an-1-2)
∴an=2an-1,
∴数列{an}是以2为首项,2为公比的等比数列,
∴an=2•2n-1=2n.
bn=log2an=log22n=n.
(2)
=
=
-
,
Tn=1-
+
-
+…+
-
=1-
=
.
(3)∵Tn=1-
,∴Tn单调递增,
当n=1时,Tn有最小值(Tn)min=1-
=
,
∵Tn=1-
>1,
∴不等式λ2-
λ>Tn对任意n∈N*恒成立,
等价于不等式λ2-
λ>1,
解得-
<λ<2,
∴λ的取值范围是(-
,2).
∴n=1时,a1=S1=2a1-2,解得a1=2.
n≥2时,an=Sn-Sn-1=2an-2-(2an-1-2)
∴an=2an-1,
∴数列{an}是以2为首项,2为公比的等比数列,
∴an=2•2n-1=2n.
bn=log2an=log22n=n.
(2)
| 1 |
| bnbn+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
Tn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
=
| n |
| n+1 |
(3)∵Tn=1-
| 1 |
| n+1 |
当n=1时,Tn有最小值(Tn)min=1-
| 1 |
| 1+1 |
| 1 |
| 2 |
∵Tn=1-
| 1 |
| n+1 |
∴不等式λ2-
| 3 |
| 2 |
等价于不等式λ2-
| 3 |
| 2 |
解得-
| 1 |
| 2 |
∴λ的取值范围是(-
| 1 |
| 2 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,考查实数的取值范围的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
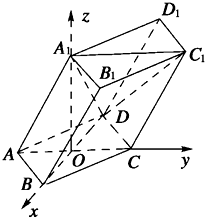 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°. 已知等腰Rt△ABC,BC⊥AC,将△ABC绕着边AB旋转θ角到△ABC′,连接CC′,D为线段CC′的中点,P是线段AB上任一点.
已知等腰Rt△ABC,BC⊥AC,将△ABC绕着边AB旋转θ角到△ABC′,连接CC′,D为线段CC′的中点,P是线段AB上任一点.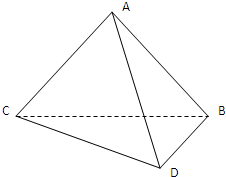 如图,平面ABC⊥平面DBC,已知AB=AC,BC=6,∠BAC=∠DBC=90°,∠BDC=60°
如图,平面ABC⊥平面DBC,已知AB=AC,BC=6,∠BAC=∠DBC=90°,∠BDC=60°