题目内容
已知cosβ=-
，则sin4β-cos4β的值为（ ）
2
| ||
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点：二倍角的余弦
专题：三角函数的求值
分析：利用同角三角函数的基本关系吧要求的式子化为（sin2β-cos2β），再利用条件、二倍角的余弦公式，计算求得结果．
解答：
解：∵cosβ=-
，
∴sin4β-cos4=（sin2β+cos2β）•（sin2β-cos2β）=（sin2β-cos2β）
=-cos2β=-[2cos2β-1]=-（2×
-1）=-
，
故选：B．
2
| ||
| 5 |
∴sin4β-cos4=（sin2β+cos2β）•（sin2β-cos2β）=（sin2β-cos2β）
=-cos2β=-[2cos2β-1]=-（2×
| 20 |
| 25 |
| 3 |
| 5 |
故选：B．
点评：本题主要考查同角三角函数的基本关系、二倍角的余弦公式的应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
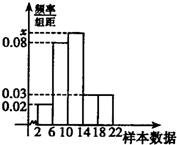为了调查学生每天零花钱的数量（钱数取整数元），以便引导学生树立正确的消费观．样本容量1000的频率分布直方图如图所示，则样本数据落在[6，14）内的频数为（ ）| A、780 | B、660 |
| C、680 | D、460 |
设集合A={1，2，3，4}，B⊆A，已知1∈B，且B中含有3个元素，则集合B有（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
定义域为R的函数f（x）=ax2+b|x|+c（a≠0）有两个单调区间，则实数a，b，c满足（ ）
| A、b2-4ac≥0且a＞0 | ||
| B、b2-4ac≥0 | ||
C、-
| ||
D、-
|
已知实数x，y满足不等式组
，则2x-y的取值范围是（ ）
|
| A、[-1，3] |
| B、[-3，-1] |
| C、[-1，6] |
| D、[-6，1] |
已知sinα=-
，则cos（
-α）的值等于（ ）
| 1 |
| 3 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
命题“存在x∈Z，使x3-2x+m≥0”的否定是（ ）
| A、存在x∈Z，使x3-2x+m≤0 |
| B、不存在x∈Z，使x3-2x+m≥0 |
| C、对任意的x∈Z，使x3-2x+m≥0 |
| D、对任意的x∈Z，使x3-2x+m＜0 |