题目内容
已知函数f(x)=mx2-m2x-mx+m2.
(1)若对于x∈[0,1],f(x)≥0恒成立,求实数m的取值范围.
(2)若对于m∈[0,1],f(x)≥0恒成立,求实数x的取值范围.
(1)若对于x∈[0,1],f(x)≥0恒成立,求实数m的取值范围.
(2)若对于m∈[0,1],f(x)≥0恒成立,求实数x的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:(1)由f(x)=mx2-m2x-mx+m2=mx2-(m2+m)x+m2,分m=0、m>0和m<0三种情况结合二次函数图象和性质列不等式求解,最后取并集求得对于x∈[0,1],f(x)≥0恒成立的实数m的取值范围;
(2)更换主元,得到f(m)=(1-x)m2+(x2-x)m,然后分x=1、x<1和x>1三种情况结合二次函数图象和性质列不等式求解,最后取并集求得对于m∈[0,1],f(x)≥0恒成立的实数x的取值范围.
(2)更换主元,得到f(m)=(1-x)m2+(x2-x)m,然后分x=1、x<1和x>1三种情况结合二次函数图象和性质列不等式求解,最后取并集求得对于m∈[0,1],f(x)≥0恒成立的实数x的取值范围.
解答:
解:f(x)=mx2-m2x-mx+m2.
(1)由f(x)=mx2-m2x-mx+m2=mx2-(m2+m)x+m2,
当m=0时,f(x)=0恒成立,满足对于x∈[0,1],f(x)≥0恒成立;
当m>0时,要使对于x∈[0,1],f(x)≥0恒成立,则
(Ⅰ)或
(Ⅱ)或
(Ⅲ).
解(Ⅰ)得:m∈∅;解(Ⅱ)得:m≥1;解(Ⅲ)得:m∈∅.
∴实数m的取值范围是[1,+∞);
当m<0时,要使对于x∈[0,1],f(x)≥0恒成立,则
,∴m<0.
综上,对于x∈[0,1],f(x)≥0恒成立的实数m的取值范围是(-∞,0]∪[1,+∞);
(2)由f(m)=mx2-m2x-mx+m2=(1-x)m2+(x2-x)m,
当x=1时,f(m)=0恒成立,满足对于m∈[0,1],f(m)≥0恒成立;
当x<1时,要使对于m∈[0,1],f(m)≥0恒成立,则
(Ⅰ)或
(Ⅱ)或
(Ⅲ)
解(Ⅰ)得:x≤0;解(Ⅱ)得:x∈∅;解(Ⅲ)得:x∈∅;
∴实数x的取值范围是(-∞,0];
当x>1时,要使对于m∈[0,1],f(m)≥0恒成立,则
,∴x>1.
综上,对于m∈[0,1],f(x)≥0恒成立的实数x的取值范围是(-∞,0]∪[1,+∞).
(1)由f(x)=mx2-m2x-mx+m2=mx2-(m2+m)x+m2,
当m=0时,f(x)=0恒成立,满足对于x∈[0,1],f(x)≥0恒成立;
当m>0时,要使对于x∈[0,1],f(x)≥0恒成立,则
|
|
|
解(Ⅰ)得:m∈∅;解(Ⅱ)得:m≥1;解(Ⅲ)得:m∈∅.
∴实数m的取值范围是[1,+∞);
当m<0时,要使对于x∈[0,1],f(x)≥0恒成立,则
|
综上,对于x∈[0,1],f(x)≥0恒成立的实数m的取值范围是(-∞,0]∪[1,+∞);
(2)由f(m)=mx2-m2x-mx+m2=(1-x)m2+(x2-x)m,
当x=1时,f(m)=0恒成立,满足对于m∈[0,1],f(m)≥0恒成立;
当x<1时,要使对于m∈[0,1],f(m)≥0恒成立,则
|
|
|
解(Ⅰ)得:x≤0;解(Ⅱ)得:x∈∅;解(Ⅲ)得:x∈∅;
∴实数x的取值范围是(-∞,0];
当x>1时,要使对于m∈[0,1],f(m)≥0恒成立,则
|
综上,对于m∈[0,1],f(x)≥0恒成立的实数x的取值范围是(-∞,0]∪[1,+∞).
点评:本题考查了函数恒成立问题,考查了二次函数的图象和性质,训练了更换主元的解题思想方法,是中档题.

练习册系列答案
相关题目
设P是双曲线
-
=1(a>0)右支上一点,其一条渐近线方程是3x-2y=0,F1、F2分别是双曲线的左、右焦点,若|PF1|=8,则|PF2|等于( )
| x2 |
| a2 |
| y2 |
| 9 |
| A、4 | B、12 |
| C、4或12 | D、2或14 |
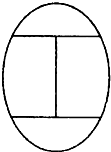 某校园有一椭圆型花坛,分成如图四块种花,现有4种不同颜色的花可供选择,要求每块地只能种一种颜色,且有公共边界的两块不能种同一种颜色,则不同的种植方法共有( )
某校园有一椭圆型花坛,分成如图四块种花,现有4种不同颜色的花可供选择,要求每块地只能种一种颜色,且有公共边界的两块不能种同一种颜色,则不同的种植方法共有( )| A、48种 | B、36种 |
| C、30种 | D、24种 |