题目内容
设P是双曲线
-
=1(a>0)右支上一点,其一条渐近线方程是3x-2y=0,F1、F2分别是双曲线的左、右焦点,若|PF1|=8,则|PF2|等于( )
| x2 |
| a2 |
| y2 |
| 9 |
| A、4 | B、12 |
| C、4或12 | D、2或14 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出双曲线的渐近线方程,由已知可得a=2,再由双曲线的定义,即可得到|PF2|.
解答:
解:双曲线
-
=1(a>0)的渐近线方程为y=±
x,
一条渐近线方程是3x-2y=0,则a=2,b=3,c=
=
.
若|PF1|=8,由双曲线的定义可得,|PF1|-|PF2|=2a=4,
则|PF2|=8-4=4.
故选:A.
| x2 |
| a2 |
| y2 |
| 9 |
| 3 |
| a |
一条渐近线方程是3x-2y=0,则a=2,b=3,c=
| a2+b2 |
| 13 |
若|PF1|=8,由双曲线的定义可得,|PF1|-|PF2|=2a=4,
则|PF2|=8-4=4.
故选:A.
点评:本题考查双曲线的定义、方程和性质,考查渐近线方程的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知平面
=(2,1),且
⊥
,则|
|=|
|,则
的坐标为( )
| a |
| a |
| b |
| a |
| b |
| b |
| A、(-1,-2) |
| B、( 1,-2) |
| C、(-1,2) |
| D、(1,-2)或(-1,2) |
某设计运动员在一次测试中射击10次,其测试成绩如表:则该运动员测试成绩的中位数为( )
| 环数 | 7 | 8 | 9 | 10 |
| 频数 | 3 | 2 | 2 | 3 |
| A、2 | B、8 | C、8.5 | D、9 |
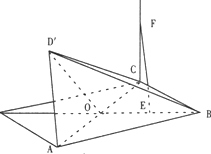 在菱形ABCD中,AC=2,BD=4,AC与BD交于0,将△ABC)沿着AC折起,使D点至点D′,且D′点到平面ABC距离为
在菱形ABCD中,AC=2,BD=4,AC与BD交于0,将△ABC)沿着AC折起,使D点至点D′,且D′点到平面ABC距离为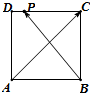 如图,正方形ABCD的边长为2,P是线段DC上的动点(含端点),则
如图,正方形ABCD的边长为2,P是线段DC上的动点(含端点),则