题目内容
若函数f（x）=（a-2）x2+2x-4的图象恒在x轴下方，求a的取值范围．
考点：函数恒成立问题
专题：函数的性质及应用
分析：对a-2=0，a-2＞0，a-2＜0进行分类，然后结合二次函数的图象列不等式组求解a的范围．
解答：
解：当a-2=0，即a=2时，f（x）=2x-4，
图象是斜率为2在y轴上的截距为-4的一条直线，不满足图象恒在x轴下方；
当a-2＞0时，函数f（x）=（a-2）x2+2x-4是二次函数，
图象是开口向上的抛物线，不满足图象恒在x轴下方；
当a-2＜0时，要保证函数f（x）=（a-2）x2+2x-4的图象恒在x轴下方，
则
，解得：a＜
．
∴满足函数f（x）=（a-2）x2+2x-4的图象恒在x轴下方的a的取值范围是（-∞，
）．
图象是斜率为2在y轴上的截距为-4的一条直线，不满足图象恒在x轴下方；
当a-2＞0时，函数f（x）=（a-2）x2+2x-4是二次函数，
图象是开口向上的抛物线，不满足图象恒在x轴下方；
当a-2＜0时，要保证函数f（x）=（a-2）x2+2x-4的图象恒在x轴下方，
则
|
| 7 |
| 4 |
∴满足函数f（x）=（a-2）x2+2x-4的图象恒在x轴下方的a的取值范围是（-∞，
| 7 |
| 4 |
点评：本题考查了函数恒成立问题，考查了分类讨论的数学思想方法，正确把握二次函数图象的形状是解答该题的关键，是基础题．
练习册系列答案
相关题目
已知平面
=（2，1），且
⊥
，则|
|=|
|，则
的坐标为（ ）
| a |
| a |
| b |
| a |
| b |
| b |
| A、（-1，-2） |
| B、（ 1，-2） |
| C、（-1，2） |
| D、（1，-2）或（-1，2） |
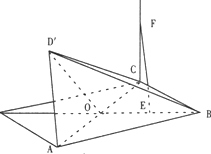在菱形ABCD中，AC=2，BD=4，AC与BD交于0，将△ABC）沿着AC折起，使D点至点D′，且D′点到平面ABC距离为