题目内容
11.已知复数z1=2+3i,z2=a+bi(a,b∈R),z3=1-4i在复平面内对应的点分别为A,B,C,O为原点,若$\overrightarrow{OC}$=2$\overrightarrow{OA}$+$\overrightarrow{OB}$,则3a-b=1.分析 根据题意,写出向量$\overrightarrow{OA}$、$\overrightarrow{OB}$、$\overrightarrow{OC}$的坐标表示,利用$\overrightarrow{OC}$=2$\overrightarrow{OA}$+$\overrightarrow{OB}$列出方程组,解方程组求出a、b的值即可.
解答 解:根据题意,$\overrightarrow{OA}$=(2,3),$\overrightarrow{OB}$=(a,b),$\overrightarrow{OC}$=(1,-4),
又$\overrightarrow{OC}$=2$\overrightarrow{OA}$+$\overrightarrow{OB}$,
∴(1,-4)=2(2,3)+(a,b)=(4+a,6+b);
即$\left\{\begin{array}{l}{4+a=1}\\{6+b=-4}\end{array}\right.$,
解得a=-3,b=-10;
∴3a-b=3×(-3)-(-10)=1.
故答案为:1.
点评 本题考查了复数的几何意义与应用问题,也考查了平面向量的坐标表示与运算问题,是基础题目.

练习册系列答案
相关题目
2.已知0<a<b<c,且a,b,c是成等比数列的整数,n为大于1的整数,则logan,logbn,logcn( )
| A. | 成等差数列 | B. | 成等比数列 | ||
| C. | 各项倒数成等差数列 | D. | 以上都不对 |
6.若sinα•cosα=$\frac{3}{10}$,且π<α<$\frac{5}{4}$π,则tanα的值为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | $\frac{1}{3}$或3 | D. | $\frac{3}{10}$ |
16.设a,b∈R,则“a>b”是“a(ea+e-a)>b(eb+e-b)”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要 条件 |
10.如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表.某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
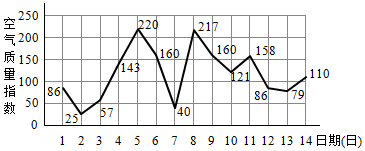
(Ⅰ)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(Ⅱ)求此人到达当日空气质量优良的概率;
(Ⅲ)设X是此人出差期间(两天)空气质量中度或重度重度污染的天数,求X的分布列与数学期望.

(Ⅰ)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(Ⅱ)求此人到达当日空气质量优良的概率;
(Ⅲ)设X是此人出差期间(两天)空气质量中度或重度重度污染的天数,求X的分布列与数学期望.
| 空气质量指数 | 污染程度 |
| 小于100 | 优良 |
| 大于100且小于150 | 轻度 |
| 大于150且小于200 | 中度 |
| 大于200且小于300 | 重度 |
| 大于300且小于500 | 严重 |
| 大于500 | 爆表 |