题目内容
11.已知等差数列{an}的前n项和为Sn,若$\overrightarrow{OB}$=a4$\overrightarrow{OA}$+a2013$\overrightarrow{OC}$,且A,B,C三点共线(O为该直线外一点),则S2016等于( )| A. | 2016 | B. | 1008 | C. | 22016 | D. | 21008 |
分析 $\overrightarrow{OB}={a_4}\overrightarrow{OA}+{a_{2013}}\overrightarrow{OC}$,且A,B,C三点共线(O为该直线外一点),利用向量共线定理可得:a4+a2013=1.由等差数列{an}的性质可得:a4+a2013=1=a1+a2016.再利用等差数列的前n项和公式即可得出.
解答 解:∵$\overrightarrow{OB}={a_4}\overrightarrow{OA}+{a_{2013}}\overrightarrow{OC}$,且A,B,C三点共线(O为该直线外一点),
∴a4+a2013=1.
由等差数列{an}的性质可得:a4+a2013=1=a1+a2016.
则S2016=$\frac{2016({a}_{1}+{a}_{2016})}{2}$=1008,
故选:B.
点评 本题考查了向量共线定理、等差数列的性质、等差数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知数列{bn}是等比数列,b9是1和3的等差中项,则b2b16=( )
| A. | 16 | B. | 8 | C. | 2 | D. | 4 |
20.从高三的期末考试成绩中,选择了五位同学A,B,C,D,E,他们的考试成绩如表:
(1)从该小组语文低于130分的同学中任选2人,求选到的2人分数都在124以下的概率;
(2)从该小组同学中任选2人,求选到的2人的语文分数都在120以上且数学分都在[100,140)中的概率.
| A | B | C | D | E | |
| 语文 | 119 | 121 | 123 | 125 | 134 |
| 数学 | 123 | 141 | 118 | 122 | 132 |
(2)从该小组同学中任选2人,求选到的2人的语文分数都在120以上且数学分都在[100,140)中的概率.
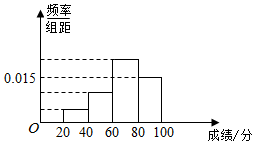 北京市某校组织学生惨叫英语测试,某班50人的成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),已知前3组的人数依次构成等比数列,第2组、第4组、第3组的人数依次构成等差数列,则及格(大于等于60分)的人数是35.
北京市某校组织学生惨叫英语测试,某班50人的成绩的频率分布直方图如图所示,数据的分组依次为[20,40),[40,60),[60,80),[80,100),已知前3组的人数依次构成等比数列,第2组、第4组、第3组的人数依次构成等差数列,则及格(大于等于60分)的人数是35.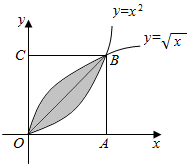 如图所示,在边长为1的正方形OABC中任取一点M,则点M恰好取自阴影部分的概率为$\frac{1}{3}$.
如图所示,在边长为1的正方形OABC中任取一点M,则点M恰好取自阴影部分的概率为$\frac{1}{3}$.