题目内容
16.设a,b∈R,则“a>b”是“a(ea+e-a)>b(eb+e-b)”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要 条件 |
分析 构造函数,f(x)=ex+e-x,分类讨论判断函数的单调性,再根据充分性和必要性判断即可.
解答 解:设f(x)=ex+e-x,
∵f′(x)=ex-e-x=$\frac{{e}^{2x}-1}{{e}^{x}}$,
当x>0时,ex>1,
∴(ex)2-1>0,
∴f′(x)>0,
∴x>0时,f(x)是增函数,
∵a>b>0,
∴f(a)>f(b),
∴ea+e-a>eb+e-b.
∴a(ea+e-a)>b(eb+e-b),
当x<0时,
∴(ex)2-1<0,
∴f′(x)<0,
∴x<0时,f(x)是减函数,
∵b<a<0,
∵f(a)<f(b),
∴ea+e-a<eb+e-b.
∴a(ea+e-a)>b(eb+e-b),
当a>0>b时,显然成立,
综上所述当a>b时,“a(ea+e-a)>b(eb+e-b)”恒成立,故充分性成立,
反之也成立,故必要性成立,
∴“a>b”是“a(ea+e-a)>b(eb+e-b)”充要条件,
故选:C.
点评 本题考查充分必要条件的判断和函数的单调性,关键是构造函数,利用导数判断函数的单调性以及分类讨论的思想,属于中档题.

练习册系列答案
相关题目
6.要得到函数y=3sin2x(x∈R)的图象,只要将函数y=3sin(2x+1)(x∈R)的图象( )
| A. | 向左平移1个位长度,纵坐标不变 | B. | 向右平移1个位长度,纵坐标不变 | ||
| C. | 向左平移$\frac{1}{2}$个位长度,纵坐标不变 | D. | 向右平移$\frac{1}{2}$个位长度,纵坐标不变 |
8.已知函数f(x)=ax3+2bx2+3cx+4d(a,b,c,d为实数,a<0,c>0)是奇函数,且当x∈[0,1]时,f(x)的值域为[0,1],则c的最大值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}+1}{4}$ |
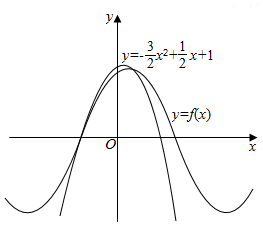 如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$).
如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)离y轴最近的零点与最大值均在抛物线y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1上,则f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$).