题目内容
已知函数f(x)=(2alnx)+2ax-x2.
(1)试确定函数f(x)在区间(0,+∞)上的单调性;
(2)设a>0,若函数y=f(x)在区间(0,+∞)上有唯一零点,试求a的值.
(1)试确定函数f(x)在区间(0,+∞)上的单调性;
(2)设a>0,若函数y=f(x)在区间(0,+∞)上有唯一零点,试求a的值.
考点:利用导数研究函数的单调性,根的存在性及根的个数判断
专题:综合题,导数的概念及应用
分析:(1)求导数,再分类讨论,根据导数的正负,可得函数f(x)在区间(0,+∞)上的单调性;
(2)x=x1为极大值,因为只有一个零点,所以f(x1)=0,再确定g(x)=2lnx+x-1是单调增的,所以至多只有一个零点,即可得出结论.
(2)x=x1为极大值,因为只有一个零点,所以f(x1)=0,再确定g(x)=2lnx+x-1是单调增的,所以至多只有一个零点,即可得出结论.
解答:
解:(1)f'(x)=
(x2-ax-a)
由f'(x)=0,得x2-ax-a=0,
所以△=a2+4a=a(a+4)
讨论a:
当-4≤a≤0时,△≤0,此时f'(x)≤0,因此函数在定义域内单调减;
当a>0时,f(x)在x>0只有一个极值点x1=
;
当x>x1时,f(x)单调减;当0<x<x1时,f(x)单调增.
a<-4时,f(x)在x>0无极值点,x>0时,f(x)单调减.
(2)由上,x=x1为极大值,因为只有一个零点,所以f(x1)=0
而x1满足x12=ax1+af(x1)=2alnx1+2ax1-ax1-a=a(2lnx1+x1-1)=0得2lnx1+x1-1=0
因为g(x)=2lnx+x-1是单调增的,所以至多只有一个零点,
而g(1)=0,所以有x1=1代入x12-ax1-a=0,得1-a-a=0,得a=
| 2 |
| x |
由f'(x)=0,得x2-ax-a=0,
所以△=a2+4a=a(a+4)
讨论a:
当-4≤a≤0时,△≤0,此时f'(x)≤0,因此函数在定义域内单调减;
当a>0时,f(x)在x>0只有一个极值点x1=
a+
| ||
| 2 |
当x>x1时,f(x)单调减;当0<x<x1时,f(x)单调增.
a<-4时,f(x)在x>0无极值点,x>0时,f(x)单调减.
(2)由上,x=x1为极大值,因为只有一个零点,所以f(x1)=0
而x1满足x12=ax1+af(x1)=2alnx1+2ax1-ax1-a=a(2lnx1+x1-1)=0得2lnx1+x1-1=0
因为g(x)=2lnx+x-1是单调增的,所以至多只有一个零点,
而g(1)=0,所以有x1=1代入x12-ax1-a=0,得1-a-a=0,得a=
| 1 |
| 2 |
点评:本题考查利用导数研究函数的单调性,考查分类讨论的数学思想,考查学生分析解决问题的能力,难度中等.

练习册系列答案
相关题目
若a,b表示直线,α表示平面,下列命题中正确的个数是( )
.
|
| A、1个 | B、2个 | C、3个 | D、4个 |
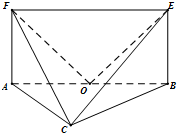 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.