题目内容
一个袋中装有四个除编号外完全相同的小球,小球的编号分别为1,2,3,4.先从袋中随机取一个球,设该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,设该球的编号为n,用(m,n)表示基本事件.
(1)求试验的基本事件的个数;
(2)求事件m+n≤4的概率;
(3)求事件n<m+2的概率.
(1)求试验的基本事件的个数;
(2)求事件m+n≤4的概率;
(3)求事件n<m+2的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:利用古典概型概率计算公式和列举法求解.
解答:
解:(1)试验的基本事件的个数为4×4=16个.
(2)试验的基本事件的个数为16个.
其中事件m+n≤4的情况有:1+1,1+2,1+3,2+1,2+2,3+1,共6个,
∴事件m+n≤4的概率p1=
=
.
(3)试验的基本事件的个数为16个,
其中事件n≥m+2的情况有(1,3),(1,4),(2,4),
∴事件n<m+2的概率p=
=
.
(2)试验的基本事件的个数为16个.
其中事件m+n≤4的情况有:1+1,1+2,1+3,2+1,2+2,3+1,共6个,
∴事件m+n≤4的概率p1=
| 6 |
| 16 |
| 3 |
| 8 |
(3)试验的基本事件的个数为16个,
其中事件n≥m+2的情况有(1,3),(1,4),(2,4),
∴事件n<m+2的概率p=
| 16-3 |
| 16 |
| 13 |
| 16 |
点评:本题考查概率的计算,解题时要认真审题,是基础题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、命题“若am2<bm2,则a<b”的逆命题是真命题 |
| B、命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x<0” |
| C、命题“p∨q”为真,则命题p,q都为真命题 |
| D、“x>1”是“x>2”的必要不充分条件 |
 函数f(x)=6cos2
函数f(x)=6cos2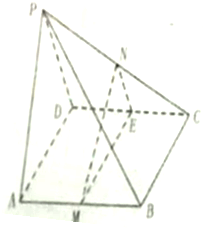 在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,M、N、E分别是AB、PC、CD的中点.
在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,M、N、E分别是AB、PC、CD的中点.