题目内容

数列{an}中，a1=2，an+1=
an+3(n为奇数)
3an(n为偶数)
，则a6=
 
．
考点：数列递推式
专题：计算题,等差数列与等比数列
分析：因为当n为正奇数时，an+1=an+3；当n为正偶数时，an+1=3an，也就是数列{an}的递推公式与n的奇偶有关系，所以通项公式不容易求，考虑用列举法，逐项来求．
解答： 解：∵a1=2，当n为正奇数时，an+1=an+3；当n为正偶数时，an+1=3an，
∴a2=a1+3=5，a3=3a2=15，a4=a3+3=18，a5=3a4=54，a6=a5+3=57．
故答案为：57．
点评：本题考查了利用数列的递推公式，求数列中的特定项的内容．
练习册系列答案
相关题目
已知函数f（x）=（2alnx）+2ax-x2．       
（1）试确定函数f（x）在区间（0，+∞）上的单调性；
（2）设a＞0，若函数y=f（x）在区间（0，+∞）上有唯一零点，试求a的值．
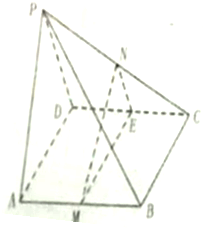在四棱锥P-ABCD中，ABCD是矩形，PA⊥平面ABCD，M、N、E分别是AB、PC、CD的中点．
（1）求证：平面MNE∥平面PAD；
（2）求证：MN∥平面PAD．
已知曲线C的极坐标方程为ρ=4cosθ，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，设直线l的参数方程为
x=5+
3
2
t
y=
1
2
t
（t为参数）．
（1）求曲线C的直角坐标方程与直线l的普通方程；
（2）设曲线C与直线l相交于P，Q两点，以PQ为一条边作曲线C的内接矩形，求该矩形的面积．
在△ABC中，角A，B，C所对的边分别为a，b，c，若a=4，b=2，cosA=
1
3
，则sinB的值为
 
．
给出以下四个命题，所有真命题的序号为
 
．
①定义在R上的函数f（x）满足f（x+1）=-f（x），则f（x）是周期函数；
②将函数y=sin2x的图象向右平移
π
3
个单位，得到函数y=sin（2x-
π
6
）的图象；
③已知数列{an}，那么“对任意的n∈N*，点Pn（n，an）都在直线y=2x+1上”是“{an}为等差数列”的充分不必要条件；
④已知回归直线的斜率的估计值为1.23，样本点的中心为（4，5），则回归直线方程为
?
y
=1.23x+0.08．
已知定义R在的函数f（x）=x|x-a|，其中a∈R，有如下判断，
①无论a取任意实数，函数f（x）的图象均过原点；
②若f（x）是奇函数，则a=0；
③当a＞2时，函数f（x）在区间（-∞，2]上的解析式是f（x）=-x2+ax；
④当a=1时，函数f（x）有最大值
1
4
；
⑤当a=2时，若函数y=f（x）-m有3个零点，则0＜m＜1．
其中正确的是
 
．
等比数列{an}中，a1=1，a4=8，则a7=
 
．
若a＞b，则下列不等式成立的是（　　）
A、ac＞bc
B、ac2＞bc2
C、
1
a
＜
1
b
D、a+c＞b+c

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网