题目内容
已知正实数a、b、c满足a2+4b2+c2=3.
(Ⅰ)求a+2b+c的最大值;
(Ⅱ)若不等式|x-5|-|x-1|≥a+2b+c恒成立,求实数x的取值范围.
(Ⅰ)求a+2b+c的最大值;
(Ⅱ)若不等式|x-5|-|x-1|≥a+2b+c恒成立,求实数x的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(I)由条件利用柯西不等式得:(a2+4b2+c2)(1+1+1)≥(a+2b+c)2,即9≥(a+2b+c)2.再根据a、b、c为正实数,求得a+2b+c的最大值.
(Ⅱ)由题意可得|x-5|-|x-1|≥(a+2b+c)max=3,可得
①;或
②;或
③.分别求得①、②、③的解集,再取并集,即得所求.
(Ⅱ)由题意可得|x-5|-|x-1|≥(a+2b+c)max=3,可得
|
|
|
解答:
解:(I)∵a2+4b2+c2=3,由柯西不等式得:(a2+4b2+c2)(1+1+1)≥(a+2b+c)2,
故有 9≥(a+2b+c)2.
再根据a、b、c为正实数,∴a+2b+c≤3,即a+2b+c的最大值为3.
(Ⅱ)∵a、b、c为正实数,不等式|x-5|-|x-1|≥a+2b+c恒成立,
∴|x-5|-|x-1|≥(a+2b+c)max=3,
∴
①;或
②;或
③.
解①求得x<1,解②求得1≤x≤
,解③求得 x∈∅,
综上可得,实数x的取值范围为(-∞,
].
故有 9≥(a+2b+c)2.
再根据a、b、c为正实数,∴a+2b+c≤3,即a+2b+c的最大值为3.
(Ⅱ)∵a、b、c为正实数,不等式|x-5|-|x-1|≥a+2b+c恒成立,
∴|x-5|-|x-1|≥(a+2b+c)max=3,
∴
|
|
|
解①求得x<1,解②求得1≤x≤
| 3 |
| 2 |
综上可得,实数x的取值范围为(-∞,
| 3 |
| 2 |
点评:本题主要考查分式不等式的解法,函数的恒成立问题,体现了等价转化和分类讨论的数学思想,属于基础题.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 函数f(x)=6cos2
函数f(x)=6cos2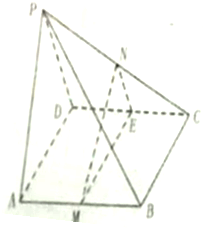 在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,M、N、E分别是AB、PC、CD的中点.
在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,M、N、E分别是AB、PC、CD的中点.