题目内容
解关于x的不等式x2-（3t+1）x+2t2+t≤0．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：不等式x2-（3t+1）x+2t2+t≤0化为（x-t）[x-（2t+1）]≤0．通过对t与-1的大小关系讨论即可得出．
解答：
解：不等式x2-（3t+1）x+2t2+t≤0化为（x-t）[x-（2t+1）]≤0．
当t＞-1时，2t+1＞t，∴不等式的解集是{x|t≤x≤2t+1}．
当t＜-1时，2t+1＜t，∴不等式的解集是{x|2t+1≤x≤t}．
当t=-1时，2t+1=t，∴不等式的解集是{x|x=-1}．
当t＞-1时，2t+1＞t，∴不等式的解集是{x|t≤x≤2t+1}．
当t＜-1时，2t+1＜t，∴不等式的解集是{x|2t+1≤x≤t}．
当t=-1时，2t+1=t，∴不等式的解集是{x|x=-1}．
点评：本题考查了一元二次不等式的解法、分类讨论的思想方法，属于基础题．
练习册系列答案
相关题目
已知不等式x2-x≤0的解集为M，且集合N={x|
＜0}，则M∩N为（ ）
| x+1 |
| x-1 |
| A、[0，1） |
| B、（0，1） |
| C、[0，1] |
| D、（-1，0] |
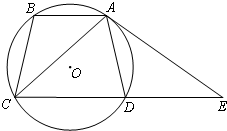如图，等腰梯形ABCD内接于⊙O，AB∥CD．过点A作⊙O的切线交CD的延长线于点E．求证：∠DAE=∠BAC．
如图，长方体ABCD-A1B1C1D1中，AB=BC=a，AA1=2a．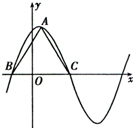
函数f（x）=6cos2