题目内容
已知f(x)=
.
(1)画出f(x)的图象;
(2)若f(m)=1,求实数m的值.
|
(1)画出f(x)的图象;
(2)若f(m)=1,求实数m的值.
考点:函数的图象
专题:函数的性质及应用
分析:由函数解析式可分别画出两个区间上的图象,通过分类讨论即可求出满足f(m)=1的自变量的值.
解答:
解:(1)作出函数f(x)的图象如图所示:

(2)如图所示,
当0≤m<2时,∵f(m)=2m-1,因此2m-1=1,解得m=1;
当m≥2时,由f(m)=m2-6m+8,因此m2-6m+8=1,解得m=3-
(舍)、m=3+
.
综上可知:当m=1或m=3+
.

(2)如图所示,
当0≤m<2时,∵f(m)=2m-1,因此2m-1=1,解得m=1;
当m≥2时,由f(m)=m2-6m+8,因此m2-6m+8=1,解得m=3-
| 2 |
| 2 |
综上可知:当m=1或m=3+
| 2 |
点评:熟练掌握分段函数的图象画法和在每一段上的函数解析式是解题的关键.另外注意分类讨论的思想方法的应用.

练习册系列答案
相关题目
数列3,7,13,21,31,…的一个通项公式是( )
| A、an=4n-1 |
| B、an=n2+n+1 |
| C、an=2+2n-n2 |
| D、an=n(n2-1) |
函数f(x)=2-x的大致图象为( )
A、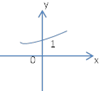 |
B、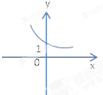 |
C、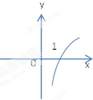 |
D、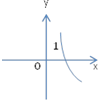 |
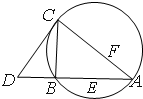 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.