Question

过点A（2，4）且与圆（x-1）²+y²=1相切的直线方程是

 

．

Answer 1

考点：圆的切线方程

专题：直线与圆

分析：分切线的斜率存在和不存在两种情况求圆的切线方程，当斜率存在时，设出切线方程的点斜式，化为一般式后由圆心到直线的距离等于半径求k的值，则切线方程可求．

解答： 解：如图，

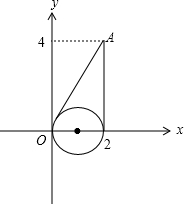
当直线的斜率不存在时，切线方程为x=2；
当直线的斜率存在时，设切线方程为y-4=k（x-2），即kx-y-2k+4=0．
由圆心（1，0）到切线的距离等于半径得：

|k-2k+4|

k2+1

=1，解得，k=

15

8

．
切线方程为：

15

8

x-y-2×

15

8

+4=0，即15x-8y+2=0．
∴过点A（2，4）且与圆（x-1）²+y²=1相切的直线方程是x=2或15x-8y+2=0．
故答案为：x=2或15x-8y+2=0．

点评：本题考查了圆的切线方程，求圆的切线方程，采用圆心到切线的距离等于圆的半径求解，考查了分类讨论的数学思想方法，是中档题．