Question

已知圆C：（x+2）²+y²=4，过M（2，0）作直线L．
（1）若L和⊙C相切，求直线L的方程；
（2）若L和⊙C相交于A，B两点，当△ACB面积最大时，求直线L的方程．

Answer 1

考点：圆的切线方程

专题：直线与圆

分析：（1）设出直线方程的点斜式，化为一般式，由圆心到直线的距离等于半径求出直线的斜率，则直线方程可求；
（2）设出直线方程，和圆的方程联立，化为关于x的一元二次方程，设出交点A，B的坐标，由根与系数关系得到A，B的横坐标的和与积，由弦长公式求出|AB|的长度，由点到直线的距离求出C到AB的距离，代入三角形的面积公式后配方，然后利用配方得到面积取最大值时的k值，则直线L的方程可求．

解答： 解：如图，

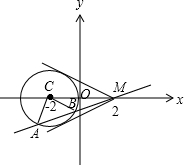
（1）设过M（2，0）的切线方程为y-0=k（x-2），即kx-y-2k=0，
由直线和圆：（x+2）²+y²=4相切，则圆心（-2，0）到直线kx-y-2k=0的距离等于圆的半径，
即

|-2k-2k|

k2+1

=2，解得：k=±

3

3

．
当k=-

3

3

时，切线方程为：x+

3

y-2=0．
当k=

3

3

时，切线方程为：x-

3

y-2=0；
（2）联立

y=kx-2k (x+2)2+y2=4

，得（1+k²）x²+（4-4k²）x+4k²=0．
设A（x₁，y₁），B（x₂，y₂），则x1+x2=

4k2-4

1+k2

，x1x2=

4k2

1+k2

，
∴|AB|=

1+k2

•

(x1+x2)2-4x1x2

=

1+k2

( 4k2-4 1+k2 )2-4• 4k2 1+k2

=

4

1+k2

•

1-3k2

，
C到AB的距离为：d=

|-2k-2k|

1+k2

=

4|k|

1+k2

．
∴S△ABC=

1

2

•

4

1+k2

•

1-3k2

•

4|k|

1+k2

=8

- 7 (1+k2)2 + 7 1+k2 -3

．
当

1

1+k2

=

1

2

，即k=±1时面积有最大值，
代入△=（4-4k²）²-16k²（1+k²）＞0成立．
∴所求的直线方程为：y=x-2或y=-x+2．

点评：本题考查了圆的切线方程，考查了直线和圆的位置关系，训练了弦长公式的用法，考查了利用基本不等式求最值，考查了学生的计算能力，是高考试卷中的压轴题．