题目内容
某省示范性高中应届毕业班有3名男生和1名女生获得了同一名牌大学的自主招生校荐资格,根据这几位考生的实际情况,估计这3名男生能通过该大学自主招生考试的概率都是
,这1名女生通过的概率是
,且这4人是否通过考试互不影响.已知通过考试的男生有a人,女生有b人.
(Ⅰ)求a=b的概率;
(Ⅱ)记ξ=a=b,求ξ的分布列和数学期望.
| 1 |
| 2 |
| 1 |
| 3 |
(Ⅰ)求a=b的概率;
(Ⅱ)记ξ=a=b,求ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:(Ⅰ)“a=b”意即“a=b=0”或“a=b=1”,且二者互斥,由此能求出a=b的概率.
(Ⅱ)由题意知ξ=0,1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
(Ⅱ)由题意知ξ=0,1,2,3,4,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答:
解:(Ⅰ)“a=b”意即“a=b=0”或“a=b=1”,且二者互斥,
∴a=b的概率P(a=b)=
(
)0(
)3+
(
)(
)2=
.
(Ⅱ)由题意知ξ=0,1,2,3,4,
P(ξ=0)=
(
)3=
,
P(ξ=1)=
(
)3+
(
)(
)2=
,
P(ξ=2)=
(
)(
)2+
(
)2(
)=
,
P(ξ=3)=
(
)2(
)+
(
)3=
,
P(ξ=4)=
(
)3=
,
∴Eξ=0×
+1×
+2×
+3×
+4×
=
.
∴a=b的概率P(a=b)=
| 2 |
| 3 |
| C | 0 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 24 |
(Ⅱ)由题意知ξ=0,1,2,3,4,
P(ξ=0)=
| 2 |
| 3 |
| C | 3 3 |
| 1 |
| 2 |
| 1 |
| 12 |
P(ξ=1)=
| 1 |
| 3 |
| C | 0 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 24 |
P(ξ=2)=
| 1 |
| 3 |
| C | 1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
P(ξ=3)=
| 1 |
| 3 |
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| C | 3 3 |
| 1 |
| 2 |
| 5 |
| 24 |
P(ξ=4)=
| 1 |
| 3 |
| C | 2 3 |
| 1 |
| 2 |
| 1 |
| 24 |
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 12 |
| 7 |
| 24 |
| 3 |
| 8 |
| 5 |
| 24 |
| 1 |
| 24 |
| 11 |
| 6 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题.

练习册系列答案
相关题目
 如图,在正方体ABCD-A1B1C1D1中,点M是棱BC的中点,则D1B与AM所成角的余弦值是
如图,在正方体ABCD-A1B1C1D1中,点M是棱BC的中点,则D1B与AM所成角的余弦值是( )
A、-
| ||||
| B、0 | ||||
C、
| ||||
D、
|
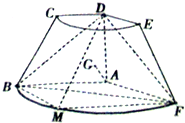 如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧
如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧
 如图,梯形BCDE中,DE∥BC,CD⊥DE,ED=DC=
如图,梯形BCDE中,DE∥BC,CD⊥DE,ED=DC=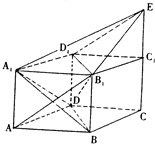 如图,已知直四棱柱ABCD-A1B1C1D1中,AB=AA1,底面ABCD为菱形,∠ADC=120°,E为CC1延长线上一点.
如图,已知直四棱柱ABCD-A1B1C1D1中,AB=AA1,底面ABCD为菱形,∠ADC=120°,E为CC1延长线上一点.