题目内容
某成品的组装工序流程图如图所示，箭头上的数字表示组装过程中所需要的时间（小时），不同车间可同时工作，同一车间不能同时做两种或两种以上的工作，则组装该产品所需要的最短时间是（ ）| A、11小时 | B、13小时 |
| C、15小时 | D、10小时 |
考点：绘制简单实际问题的流程图
专题：计算题,算法和程序框图
分析：由已知中的工序流程图，我们可以计算出每条组装劳工序从开始到结束的时间，进而根据从工程设计到结束试生产需要的最短时间为并联事件中的最大值，串联事件的和，进而得到答案．
解答：
解：A到E的时间，为2+4=6小时，或5小时，
A经C到D的时间为3+4=7小时，
故A到F的最短时间就为9小时，
则A经F到G的时间为9+2=11小时，
即组装该产品所需要的最短时间是11小时，
故选：A．
A经C到D的时间为3+4=7小时，
故A到F的最短时间就为9小时，
则A经F到G的时间为9+2=11小时，
即组装该产品所需要的最短时间是11小时，
故选：A．
点评：本题考查的知识点是工序流程图，完成本题的关键是要认真分析所给流程图，从中获得正信息后，结合所给条件进行分析．
练习册系列答案
阅读快车系列答案
相关题目
经过点A（1，0），B（0，-1）的直线方程为（ ）
| A、y=x+1 |
| B、y=x-1 |
| C、y=-x+1 |
| D、y=-x-1 |
如图，在正方体ABCD-A1B1C1D1中，点M是棱BC的中点，则D1B与AM所成角的余弦值是（ ）
A、-
| ||||
| B、0 | ||||
C、
| ||||
D、
|
已知直线l的方程为
x-y+
=0，则它的倾斜角为（ ）
| 3 |
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
将一枚骰子连续抛掷两次，则向上点数之差的绝对值不大于3的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设实数a，b，c满足a+b+c=6，则a，b，c中（ ）
| A、至多有一个不大于2 |
| B、至少有一个不小于2 |
| C、至多有两个不小于2 |
| D、至少有两个不小于2 |
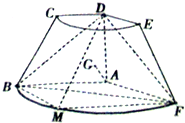如图，在直角梯形ABCD中，AB=AD=2，把此梯形绕其直角边AD旋转120°得到如图所示的几何体，点G是∠BDF平分线上任意一点（异于点D），点M是弧