题目内容
已知向量
=(2cos(x-
),-2sin(x-
)),
=(cos(x-
),-sin(x+
)),f(x)=
•
-2.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[-
,
]的最值.
| a |
| π |
| 6 |
| π |
| 4 |
| b |
| π |
| 6 |
| π |
| 4 |
| a |
| b |
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[-
| π |
| 12 |
| π |
| 12 |
考点:平面向量数量积的运算,三角函数中的恒等变换应用
专题:三角函数的图像与性质,平面向量及应用
分析:(1)利用数量积运算、倍角公式、两角和差的正弦公式、三角函数的周期公式即可得出;
(2)利用正弦函数的单调性即可得出.
(2)利用正弦函数的单调性即可得出.
解答:
解:(1)f(x)=
•
-2
=2cos2(x-
)+2sin(x-
)sin(x+
)
=1+cos(2x-
)-sin(2x+
)-2
=cos(2x-
)-cos2x-1
=sin(2x-
)-1
∴函数f(x)的最小正周期是T=
=π.
(2)∵x∈[-
,
],∴-
≤x≤0,
∴-
≤sin(2x-
)≤0,
∴f(x)的最大值是0,最小值是-
-1.
| a |
| b |
=2cos2(x-
| π |
| 6 |
| π |
| 4 |
| π |
| 4 |
=1+cos(2x-
| π |
| 3 |
| π |
| 2 |
=cos(2x-
| π |
| 3 |
=sin(2x-
| π |
| 6 |
∴函数f(x)的最小正周期是T=
| 2π |
| 2 |
(2)∵x∈[-
| π |
| 12 |
| π |
| 12 |
| π |
| 3 |
∴-
| ||
| 2 |
| π |
| 6 |
∴f(x)的最大值是0,最小值是-
| ||
| 2 |
点评:本题考查了数量积运算、倍角公式、两角和差的正弦公式、三角函数的周期公式、正弦函数的单调性等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
若sin(α-
)=
,则cos(2α-
)的值是( )
| π |
| 6 |
| 1 |
| 3 |
| π |
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知直线l的方程为
x-y+
=0,则它的倾斜角为( )
| 3 |
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设实数a,b,c满足a+b+c=6,则a,b,c中( )
| A、至多有一个不大于2 |
| B、至少有一个不小于2 |
| C、至多有两个不小于2 |
| D、至少有两个不小于2 |
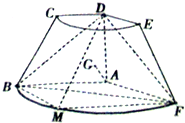 如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧
如图,在直角梯形ABCD中,AB=AD=2,把此梯形绕其直角边AD旋转120°得到如图所示的几何体,点G是∠BDF平分线上任意一点(异于点D),点M是弧
 如图,梯形BCDE中,DE∥BC,CD⊥DE,ED=DC=
如图,梯形BCDE中,DE∥BC,CD⊥DE,ED=DC=