题目内容
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则:每人从备选的10道题中一次性抽取3道题独立作答,至少答对2道题即闯关成功.已知10道备选题中,甲只能答对其中的6道题,乙答对每道题的概率都是
.
(Ⅰ)求甲闯关成功的概率;
(Ⅱ)设乙答对题目的个数为X,求X的分布列及数学期望.
| 1 |
| 3 |
(Ⅰ)求甲闯关成功的概率;
(Ⅱ)设乙答对题目的个数为X,求X的分布列及数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)利用互斥事件概率加法公式能求出甲闯关成功的概率.
(Ⅱ)依题意X~B(3,
),X可能取的值为0,1,2,3,由此能求出X的分布列及数学期望.
(Ⅱ)依题意X~B(3,
| 1 |
| 3 |
解答:
解:(Ⅰ)设“甲闯关成功”为事件A,
则甲闯关成功的概率P(A)=
=
.…(4分)
(Ⅱ)依题意X~B(3,
),X可能取的值为0,1,2,3,
P(X=0)=
(1-
)3=
,
P(X=1)=
•
•(1-
)2=
,
P(X=2)=
(
)2(1-
)=
,
P(X=3)=
(
)3=
,
∴X的分布列为:
…(10分)
EX=np=3×
=1.…(12分)
则甲闯关成功的概率P(A)=
| ||||||
|
| 2 |
| 3 |
(Ⅱ)依题意X~B(3,
| 1 |
| 3 |
P(X=0)=
| C | 0 3 |
| 1 |
| 3 |
| 8 |
| 27 |
P(X=1)=
| C | 1 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
P(X=2)=
| C | 2 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 9 |
P(X=3)=
| C | 3 3 |
| 1 |
| 3 |
| 1 |
| 27 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
EX=np=3×
| 1 |
| 3 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,是历年高考的必考题型.

练习册系列答案
相关题目
在等边△ABC的边BC上任取一点p,则S△ABP≤
S△ABC的概率是( )
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|




 如图,四棱锥P-ABCD的底面是边长为2的正方形,PD⊥平面ABCD,PD=2,E为AB的中点.
如图,四棱锥P-ABCD的底面是边长为2的正方形,PD⊥平面ABCD,PD=2,E为AB的中点.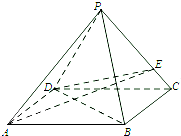 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,平面PBD⊥平面ABCD,AD=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,平面PBD⊥平面ABCD,AD=2,PD=2