题目内容
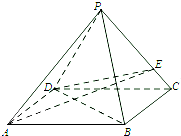 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,平面PBD⊥平面ABCD,AD=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,平面PBD⊥平面ABCD,AD=2,PD=2| 5 |
(Ⅰ)求证:AD⊥PB;
(Ⅱ)E是侧棱PC上一点,记
| PE |
| PC |
考点:直线与平面垂直的性质,空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明AD⊥BD,利用平面PBD⊥平面ABCD,交线为BD,可得AD⊥平面PBD,从而AD⊥PB;
(Ⅱ)作EF∥BC,交PB于点F,连接AF,连接DF,△PBD中,由余弦定理求得cos∠BPD=
,即可得出结论.
(Ⅱ)作EF∥BC,交PB于点F,连接AF,连接DF,△PBD中,由余弦定理求得cos∠BPD=
| 3 | ||
2
|
解答:
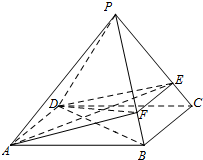 (Ⅰ)证明:在△ABD中,∵AD=2,AB=4,∠BAD=60°,
(Ⅰ)证明:在△ABD中,∵AD=2,AB=4,∠BAD=60°,
∴由余弦定理求得BD=2
.
∴AD2+BD2=AB2,∴AD⊥BD.
∵平面PBD⊥平面ABCD,交线为BD,
∴AD⊥平面PBD,
∴AD⊥PB.…6分
(Ⅱ)解:作EF∥BC,交PB于点F,连接AF,
由EF∥BC∥AD可知A,D,E,F四点共面,
连接DF,所以由(Ⅰ)的结论可知,PB⊥平面ADE当且仅当PB⊥DF.
在△PBD中,由PB=4,BD=2
,PD=2
,
余弦定理求得cos∠BPD=
,
∴在RT△PDF中,PF=PDcos∠BPD=3,
因此λ=
=
=
.…12分.
 (Ⅰ)证明:在△ABD中,∵AD=2,AB=4,∠BAD=60°,
(Ⅰ)证明:在△ABD中,∵AD=2,AB=4,∠BAD=60°,∴由余弦定理求得BD=2
| 3 |
∴AD2+BD2=AB2,∴AD⊥BD.
∵平面PBD⊥平面ABCD,交线为BD,
∴AD⊥平面PBD,
∴AD⊥PB.…6分
(Ⅱ)解:作EF∥BC,交PB于点F,连接AF,
由EF∥BC∥AD可知A,D,E,F四点共面,
连接DF,所以由(Ⅰ)的结论可知,PB⊥平面ADE当且仅当PB⊥DF.
在△PBD中,由PB=4,BD=2
| 3 |
| 5 |
余弦定理求得cos∠BPD=
| 3 | ||
2
|
∴在RT△PDF中,PF=PDcos∠BPD=3,
因此λ=
| PE |
| PC |
| PF |
| PB |
| 3 |
| 4 |
点评:本题考查立体几何有关知识,考查线面、面面垂直,考查运算能力,属于中档题.

练习册系列答案
相关题目
观察数列1,
,
,
,
,
,
,
,
,
,…,则数
将出现在此数列( )
| 1 |
| 2 |
| 2 |
| 1 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 1 |
| 4 |
| 2 |
| 3 |
| 3 |
| 2 |
| 4 |
| 1 |
| 2 |
| 6 |
| A、第21项 | B、第22项 |
| C、第23项 | D、第24项 |
 如图,四边形ABCD为矩形,四边形ADEF为梯形,FE
如图,四边形ABCD为矩形,四边形ADEF为梯形,FE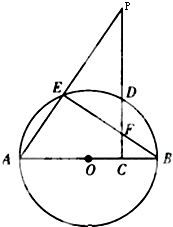 如图,AB为圆O的直径,P为圆O外一点,过P点作PC⊥AB于C,交圆O于D点,PA交圆O于E点,BE交PC于F点.
如图,AB为圆O的直径,P为圆O外一点,过P点作PC⊥AB于C,交圆O于D点,PA交圆O于E点,BE交PC于F点.