题目内容
2.已知定义域为R的偶函数f(x)满足对任意的x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-(x-2)2+1.若函数y=f(x)-a(x-$\frac{11}{12}$)在(0,+∞)上恰有三个零点,则实数a的取值范围是( )| A. | ($\frac{1}{3}$,3) | B. | ($\frac{1}{3}$,$\frac{4}{3}$) | C. | (3,12) | D. | ($\frac{4}{3}$,12) |
分析 令x=-1,求出f(1),可得函数f(x)的周期为2,根据函数与方程之间的关系,转化为两个函数的交点问题,利用数形结合进行求解即可.
解答 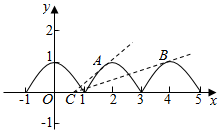 解:∵f(x+2)=f(x)-f(1),
解:∵f(x+2)=f(x)-f(1),
且f(x)是定义域为R的偶函数,
令x=-1可得f(-1+2)=f(-1)-f(1),
又f(-1)=f(1),
∴f(1)=0 则有f(x+2)=f(x),
∴f(x)是最小正周期为2的偶函数.
当x∈[2,3]时,f(x)=-(x-2)2+1,
若x∈[0,1],则x+2∈[2,3],
则f(x)=f(x+2)=-(x+2-2)2+1=-x2+1,
即f(x)=-x2+1,x∈[0,1],
若x∈[-1,0],则-x∈[0,1],
即f(-x)=-x2+1=f(x),
即f(x)=-x2+1,x∈[-1,0],
综上f(x)=-x2+1,x∈[-1,1],
由函数y=f(x)-a(x-$\frac{11}{12}$)=0,
得函数f(x)=a(x-$\frac{11}{12}$),
设y=a(x-$\frac{11}{12}$),
作出函数f(x)和y=a(x-$\frac{11}{12}$)的图象如图,
要使函数y=f(x)-a(x-$\frac{11}{12}$)在(0,+∞)上恰有三个零点,
则a>0,
当x∈[1,2],则x-2∈[-1,0],
则f(x)=f(x-2)=-(x-2)2+1,x∈[1,2],
当x∈[3,4],则x-2∈[1,2],
则f(x)=f(x-2)=-(x-4)2+1,x∈[3,4],
由-(x-2)2+1=a(x-$\frac{11}{12}$)整理得x2+(a-4)x+3-$\frac{11}{12}$a=0,
由判别式△=(a-4)2-4(3-$\frac{11}{12}$a)=0,
整理得3a2-13a+12=0得a=3(由图象知不合适)或a=$\frac{4}{3}$,
由-(x-4)2+1=a(x-$\frac{11}{12}$)整理得x2+(a-8)x+15-$\frac{11}{12}$a=0,
由判别式△=(a-8)2-4(15-$\frac{11}{12}$a)=0,
整理得3a2-37a+12=0得a=12(由图象知不合适)或a=$\frac{1}{3}$,
综上,要使函数y=f(x)-a(x-$\frac{11}{12}$)在(0,+∞)上恰有三个零点,
则$\frac{1}{3}$<a<$\frac{4}{3}$,
故选:B
点评 本题主要考查方程根的个数的判断,利用函数与方程之间的关系转化为两个函数的交点个数问题,利用数形结合以及分类讨论是解决本题的关键.综合性较强,运算量较大.

 备战中考寒假系列答案
备战中考寒假系列答案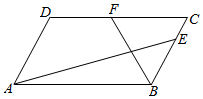 在平行四边形ABCD中,AB=4,AD=3,∠DAB=$\frac{π}{3}$,点E,F分别在BC,DC边上,且$\overrightarrow{BE}$=$2\overrightarrow{EC}$,$\overrightarrow{DF}$=$\overrightarrow{FC}$,则$\overrightarrow{AE}$$•\overrightarrow{BF}$=( )
在平行四边形ABCD中,AB=4,AD=3,∠DAB=$\frac{π}{3}$,点E,F分别在BC,DC边上,且$\overrightarrow{BE}$=$2\overrightarrow{EC}$,$\overrightarrow{DF}$=$\overrightarrow{FC}$,则$\overrightarrow{AE}$$•\overrightarrow{BF}$=( )| A. | $-\frac{8}{3}$ | B. | -1 | C. | 2 | D. | $\frac{10}{3}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
| A. | 24 | B. | 27 | C. | 15 | D. | 54 |
| A. | 5 | B. | 25 | C. | 120 | D. | 625 |
| A. | C${\;}_{12}^{8}$ | B. | C${\;}_{12}^{8}$24 | C. | -C${\;}_{12}^{9}$ | D. | -C${\;}_{12}^{9}$23 |