题目内容
△ABC中a、b、c分别为∠A、∠B、∠C的对边.如果a、b、c满足2b=a+c,∠B=30°,△ABC的面积为
,那么b= .
| 3 |
| 2 |
考点:正弦定理
专题:解三角形
分析:将2b=a+c平方后整理得a2+c2=4b2-2ac,利用三角形面积求得ac的值,再把a2+c2=4b2-2ac,代入余弦定理求得b的值.
解答:
解:由题意得2b=a+c,平方得a2+c2=4b2-2ac,
又∠B=30°,△ABC的面积为
,
所以S△ABC=
acsinB=
×ac×
=
,得ac=6,
则a2+c2=4b2-12.
由余弦定理得,b2=a2+c2-2accosB,
所以b2=4b2-12-2×6×
,
化简得,b2=4+2
,
又b为边长,则b=1+
,
故答案为:1+
.
又∠B=30°,△ABC的面积为
| 3 |
| 2 |
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
则a2+c2=4b2-12.
由余弦定理得,b2=a2+c2-2accosB,
所以b2=4b2-12-2×6×
| ||
| 2 |
化简得,b2=4+2
| 3 |
又b为边长,则b=1+
| 3 |
故答案为:1+
| 3 |
点评:本题考查解三角形的问题,解题过程中常需要正弦定理,余弦定理,三角形面积公式等知识,注意整体代换.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
设集合S={x|2x>
},T={x|-4≤x≤1},则S∩T=( )
| 1 |
| 4 |
| A、[-4,+∞) |
| B、(-2,+∞) |
| C、[-4,1] |
| D、(-2,1] |
设k<-1,则关于x、y的方程(1-k)x2+y2=k2-1所表示的曲线是( )
| A、实轴在x轴上的双曲线 |
| B、实轴在y轴上的双曲线 |
| C、长轴在x轴上的椭圆 |
| D、长轴在y轴上的椭圆 |
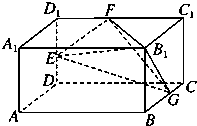 如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.
如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.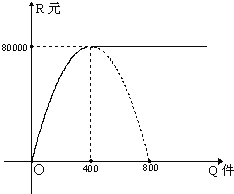 某工厂生产某种产品,固定成本为20000元,每生产一件产品,成本增加100元.已知总收益R是年产量Q(件)的函数,其图象(图中实线部分)如下:当年产量Q在[0,400]内时,为抛物线的一段;当年产量Q>400件时,为一条射线.
某工厂生产某种产品,固定成本为20000元,每生产一件产品,成本增加100元.已知总收益R是年产量Q(件)的函数,其图象(图中实线部分)如下:当年产量Q在[0,400]内时,为抛物线的一段;当年产量Q>400件时,为一条射线.