题目内容
1.幂函数f(x)的图象过点$({2,\sqrt{2}})$,则$f({\frac{1}{2}})$=( )| A. | $\sqrt{2}$ | B. | 4 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{4}$ |
分析 由于幂函数f(x)=xα的图象过点(2,$\sqrt{2}$),把此点的坐标代入解得α,从而求出f($\frac{1}{2}$)的值即可.
解答 解:设幂函数f(x)=xα,
∵图象过点(2,$\sqrt{2}$),
∴$\sqrt{2}$=2α,解得α=$\frac{1}{2}$
故f(x)=$\sqrt{x}$,f($\frac{1}{2}$)=$\frac{\sqrt{2}}{2}$,
故选:C.
点评 本题考查了幂函数的定义,属于基础题.

练习册系列答案
相关题目
12.已知函数f(x)=lnx+$\frac{1}{2}$ax2-2x有两个极值点,则a的取值范围是( )
| A. | (-∞,1) | B. | (0,2) | C. | (0,1) | D. | (0,3) |
6.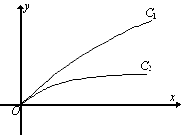 如图,当参数λ=λ1,λ2时,连续函数y=$\frac{x}{1+λx}$(x≥0)的图象分别对应曲线C1和C2,则( )
如图,当参数λ=λ1,λ2时,连续函数y=$\frac{x}{1+λx}$(x≥0)的图象分别对应曲线C1和C2,则( )
 如图,当参数λ=λ1,λ2时,连续函数y=$\frac{x}{1+λx}$(x≥0)的图象分别对应曲线C1和C2,则( )
如图,当参数λ=λ1,λ2时,连续函数y=$\frac{x}{1+λx}$(x≥0)的图象分别对应曲线C1和C2,则( )| A. | 0<λ2<λ1 | B. | λ2<λ1<0 | C. | λ1<λ2<0 | D. | 0<λ1<λ2 |
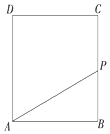 如图所示,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过顶点B,C,D再回到A.设x表示P点的路程,y表示PA的长度,求y关于x的函数关系式.
如图所示,动点P从边长为1的正方形ABCD的顶点A出发,顺次经过顶点B,C,D再回到A.设x表示P点的路程,y表示PA的长度,求y关于x的函数关系式.