题目内容
16.如图1所示,在矩形ABCD中,AB=4$\sqrt{5}$,AD=2$\sqrt{5}$,BD是对角线,过A点作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到达点P的位置(图2),且PB=2$\sqrt{17}$.
(1)求证:PO⊥平面ABCE;
(2)过点C作一平面与平面PAE平行,作出这个平面,写出作图过程;
(3)在(2)的结论下,求出四棱锥P-ABCE介于这两平行平面间部分的体积.
分析 (1)推导出PO⊥OB,PO⊥AE,由此能证明PO⊥平面ABCE.
(2)过点C作AE的平行线交AB于点F,过点F作PA的平行线交PB于点G,连结CG,能得到所求的平面.
(3)所求几何体的体积为V=VP-ABCD-VG-BCF,由此能求出结果.
解答 证明:(1)在图1中,AB=4$\sqrt{5}$,AD=2$\sqrt{5}$,则BD=10,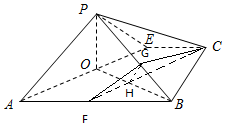
又AD2=DO•BD,∴DO=2,OB=8,
在图2中,PO=DO=2,PO2+OB2=22+82=68=PB2,
∴PO⊥OB,
又∵PO⊥AE,AE∩OB=O,
∴PO⊥平面ABCE.
解:(2)过点C作AE的平行线交AB于点F,过点F作PA的平行线交PB于点G,
连结CG,
则平面CFG为过点C与平面PAE平行的平面.
(3)在图1中,∵△DOE∽△DCB,∴DE=5,
∴S△ADE=5,S梯形ABCE=SABCD-S△ADE=35,S△BCF=S△ADE=5,
设CF∩OB于H,连结GH,
则$\frac{GH}{PO}=\frac{BH}{OB}$,解得GH=$\frac{1}{2}$,
∴所求几何体的体积为:
V=VP-ABCD-VG-BCF=$\frac{1}{3}•{S}_{梯形ABCE}•PO-\frac{1}{3}•{S}_{△BCF}•GH$
=$\frac{1}{3}×35×2-\frac{1}{3}×5×\frac{1}{2}$=$\frac{45}{2}$.
点评 本题考查线面垂直的证明,考查满足条件的平面的作法,考查向何体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
6.集合{x∈N|x≤3}还可以表示为( )
| A. | {0,1,2,3} | B. | {2,1,3} | C. | {1,2,3,4} | D. | {x|0≤x≤3} |
7.已知f(x)是定义在R上周期为2的奇函数,当x∈(0,1)时,f(x)=4x-1,则f(log4$\frac{1}{32}$)( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
4.方程(a-1)x2+(2-a)y2=(a-1)(2-a)中,当1<a<2时,它表示( )
| A. | 椭圆或圆 | B. | 双曲线 | C. | 椭圆 | D. | 圆 |
11.过(2,2)点与双曲线x2$-\frac{y^2}{4}=1$有共同渐近线的双曲线方程为( )
| A. | x2$-\frac{y^2}{4}=-1$ | B. | $\frac{x^2}{4}-{y^2}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{12}=1$ | D. | $\frac{y^2}{12}-\frac{x^2}{3}=1$ |
1.幂函数f(x)的图象过点$({2,\sqrt{2}})$,则$f({\frac{1}{2}})$=( )
| A. | $\sqrt{2}$ | B. | 4 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{4}$ |