题目内容

9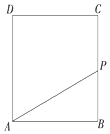．如图所示，动点P从边长为1的正方形ABCD的顶点A出发，顺次经过顶点B，C，D再回到A．设x表示P点的路程，y表示PA的长度，求y关于x的函数关系式．

分析 分别讨论点P在正方形各边上的位置，建立PA的关系时，得到y关于x的函数解析式．

解答 解：当P在AB上时，即0≤x≤1，y=PA=x；
当P在BC上时，即1＜x≤2，y=PA=$\sqrt{A{B}^{2}+B{P}^{2}}$=$\sqrt{1+（x-1）^{2}}$；
当P在CD上时，即2＜x≤3，y=PA=$\sqrt{A{D}^{2}+D{P}^{2}}$=$\sqrt{{1}^{1}+（3-x）^{2}}$；
当P在DA上时，即3＜x≤4，y=PA=4-x．
所以y关于x的函数解析式为y=$\left\{\begin{array}{l}{x，0≤x≤1}\\{\sqrt{{x}^{2}-2x+2}，1＜x≤2}\\{\sqrt{{x}^{2}-6x+10}，2＜x≤3}\\{4-x，3＜x≤4}\end{array}\right.$．

点评 本题的考点是函数解析式的求法以及函数的简单应用，本题要注意对点P进行分类讨论，从而得出一个分段函数

练习册系列答案
相关题目
19．求值：
（1）2$\sqrt{3}$×$\root{3}{1.5}$×$\root{6}{12}$
（2）已知x+$\frac{1}{x}$=3，求x${\;}^{\frac{1}{2}}$+x${\;}^{-\frac{1}{2}}$的值．
20．已知向量$\overrightarrow a=（1，2），\overrightarrow b=（1，0），\overrightarrow c=（3，-4）$，若λ为实数且$（\overrightarrow a+λ\overrightarrow b）$∥$\overrightarrow c$，则λ=$-\frac{5}{2}$．
17．给出下列函数①$f（x）=（\frac{1}{2}）^{x}$； ②f（x）=x2； ③f（x）=x3； ④$f（x）={x}^{\frac{1}{2}}$；⑤f（x）=log2x．其中满足条件f $（\frac{{x}_{1}+{x}_{2}}{2}）$＞$\frac{f（{x}_{1}）+f（{x}_{2}）}{2}$  （0＜x1＜x2）的函数的序号是④⑤．
4．方程（a-1）x2+（2-a）y2=（a-1）（2-a）中，当1＜a＜2时，它表示（　　）
A．椭圆或圆B．双曲线C．椭圆D．圆
14．已知a，b，c分别是△ABC的内角A，B，C的对边，向量$\overrightarrow{m}$=（tanA+tanB，-tanB），$\overrightarrow{n}$=（b，2c），且$\overrightarrow{m}⊥\overrightarrow{n}$
（1）求角A的大小；
（2）若$a=\sqrt{13}$，△ABC的面积为$3\sqrt{3}$，求b，c的值．
1．幂函数f（x）的图象过点$（{2，\sqrt{2}}）$，则$f（{\frac{1}{2}}）$=（　　）
A．$\sqrt{2}$B．4C．$\frac{{\sqrt{2}}}{2}$D．$\frac{1}{4}$
18．已知函数$f（x）=\frac{{{x^2}+a}}{x}$（常数a∈R）．
（1）判断函数f（x）的奇偶性，并证明；
（2）若f（1）=2，证明函数f（x）在（1，+∞）上是增函数．
1．将函数 y=cos（2x+$\frac{3π}{2}$）的图象向左平移 $\frac{π}{4}$个单位长度，再向上平移 1个单位长度后，所得图象的函数解析式是y=cos2x+1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网